
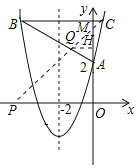
【题目】如图,抛物线y=x2+bx+c与y轴交于点A(0,2),对称轴为直线x=﹣2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式.
(2)点P在x轴上,直线CP将△ABC面积分成2:3两部分,请直接写出P点坐标.

【答案】(1)抛物线的解析式为y=x2+4x+2;(2)P的坐标为(﹣6,0)或(﹣13,0).
【解析】(1)由对称轴直线x=2,以及A点坐标确定出b与c的值,即可求出抛物线解析式;
(2)由抛物线的对称轴及BC的长,确定出B与C的横坐标,代入抛物线解析式求出纵坐标,确定出B与C坐标,利用待定系数法求出直线AB解析式,作出直线CP,与AB交于点Q,过Q作QH⊥y轴,与y轴交于点H,BC与y轴交于点M,由已知面积之比求出QH的长,确定出Q横坐标,代入直线AB解析式求出纵坐标,确定出Q坐标,再利用待定系数法求出直线CQ解析式,即可确定出P的坐标.
(1)由题意得:x=﹣![]() =﹣
=﹣![]() =﹣2,c=2,
=﹣2,c=2,
解得:b=4,c=2,
则此抛物线的解析式为y=x2+4x+2;
(2)∵抛物线对称轴为直线x=﹣2,BC=6,
∴B横坐标为﹣5,C横坐标为1,
把x=1代入抛物线解析式得:y=7,
∴B(﹣5,7),C(1,7),
设直线AB解析式为y=kx+2,
把B坐标代入得:k=﹣1,即y=﹣x+2,
作出直线CP,与AB交于点Q,过Q作QH⊥y轴,与y轴交于点H,BC与y轴交于点M,
可得△AQH∽△ABM,
∴![]() ,
,
∵点P在x轴上,直线CP将△ABC面积分成2:3两部分,
∴AQ:QB=2:3或AQ:QB=3:2,即AQ:AB=2:5或AQ:QB=3:5,
∵BM=5,
∴QH=2或QH=3,
当QH=2时,把x=﹣2代入直线AB解析式得:y=4,
此时Q(﹣2,4),直线CQ解析式为y=x+6,令y=0,得到x=﹣6,即P(﹣6,0);
当QH=3时,把x=﹣3代入直线AB解析式得:y=5,
此时Q(﹣3,5),直线CQ解析式为y=![]() x+
x+![]() ,令y=0,得到x=﹣13,此时P(﹣13,0),
,令y=0,得到x=﹣13,此时P(﹣13,0),
综上,P的坐标为(﹣6,0)或(﹣13,0).


科目:初中数学 来源: 题型:
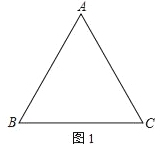
【题目】如图,△ABC是边长为6cm的等边三角形,点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动,与此同时,点E从线段BC的某个端点出发,以b cm/s速度在线段BC上运动,当D到达A点后,D、E运动停止,运动时间为t(秒).
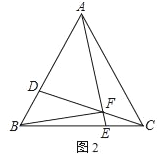
(1)如图1,若a=b=1,点E从C出发沿C→B方向运动,连AE、CD,AE、CD交于F,连BF.当0<t<6时:
①求∠AFC的度数;
②求![]() 的值;
的值;
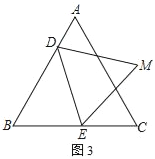
(2)如图2,若a=1,b=2,点E从B点出发沿B→C方向运动,E点到达C点后再沿C→B方向运动.当t≥3时,连DE,以DE为边作等边△DEM,使M、B在DE两侧,求M点所经历的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.

(1)甲车间每天加工零件为_____件,图中d值为_____.
(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.
(3)甲车间加工多长时间时,两车间加工零件总数为1000件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠C=90°,AC=BC=7,D是AB的中点,点E在AC上,点F在BC上,DE=DF,若BF=4,则EF=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位歌手进入“我是歌手”的决赛,他们通过抽签来决定演唱顺序.
(1)求甲第一位出场的概率;
(2)求甲比乙先出场的概率,请用列表或画树状图的方法进行分析说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com