
【题目】已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④![]() ≥2.
≥2.
其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
由a>0可知抛物线开口向上,再根据抛物线与x轴最多有一个交点可c>0,由此可判断①,根据抛物线的对称轴公式x=﹣![]() 可判断②,由ax2+bx+c≥0可判断出ax2+bx+c+1≥1>0,从而可判断③,由题意可得a﹣b+c>0,继而可得a+b+c≥2b,从而可判断④.
可判断②,由ax2+bx+c≥0可判断出ax2+bx+c+1≥1>0,从而可判断③,由题意可得a﹣b+c>0,继而可得a+b+c≥2b,从而可判断④.
①∵抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点,
∴抛物线与y轴交于正半轴,
∴c>0,
∴abc>0,故①正确;
②∵0<2a≤b,
∴![]() >1,
>1,
∴﹣![]() <﹣1,
<﹣1,
∴该抛物线的对称轴在x=﹣1的左侧,故②错误;
③由题意可知:对于任意的x,都有y=ax2+bx+c≥0,
∴ax2+bx+c+1≥1>0,即该方程无解,故③正确;
④∵抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点,
∴当x=﹣1时,y>0,
∴a﹣b+c>0,
∴a+b+c≥2b,
∵b>0,
∴![]() ≥2,故④正确,
≥2,故④正确,
综上所述,正确的结论有3个,
故选C.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①;cos(α+β)=cosαcosβ﹣sinαsinβ②;tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,
如:tan105°=tan(45°+60°)=![]() =
=![]() =
=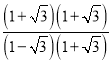 =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
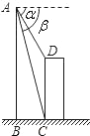
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为3的⊙O经过等边△ABO的顶点A、B,点P为半径OB上的动点,连接AP,过点P作PC⊥AP交⊙O于点C,当∠ACP=30°时,AP的长为( )
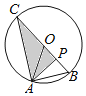
A. 3B. 3或![]() C.
C. ![]() D. 3或
D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() .
.
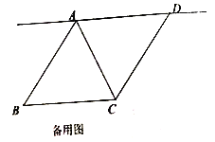
(1)求![]() 的长;
的长;
(2)点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ),
),![]() 交
交![]() 于点
于点![]() .
.
①当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
②连接![]() 、
、![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
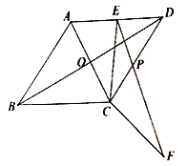
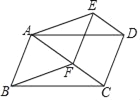
【题目】如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课堂上,小斐同学和小可同学分别拿着一大一小两个等腰直角三角板,可分别记做![]() 和
和![]() ,其中
,其中![]() .
.
问题的产生:
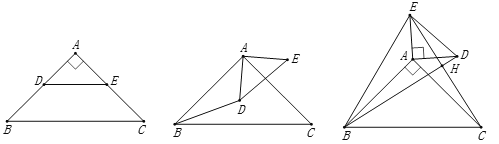
两位同学先按照如图摆放,点![]() 在
在![]() 上,发现
上,发现![]() 和
和![]() 在数量和位置关系上分别满足
在数量和位置关系上分别满足![]() ,
,![]() .
.
问题的探究:
(1)将![]() 绕点
绕点![]() 逆时针旋转一定角度.如图.点
逆时针旋转一定角度.如图.点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,连结
外部,连结![]() ,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
问题的延伸:
继续将![]() 绕点
绕点![]() 逆时针旋转.如图.点
逆时针旋转.如图.点![]() 都在
都在![]() 外部,连结
外部,连结![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() 点.
点.
(2)若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
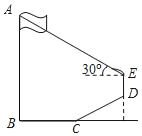
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图为某班35名学生投篮成绩的条型统计图,其中上面部分数据缺损导致数据不完全.已知此班学生投篮成绩的中位数是5,则根据统计图的数据,无法确定下列哪一选项中的数值( )
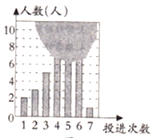
A. 4球(不含4球)以下的人数B. 5球(不含5球)以下的人数
C. 6球(不含6球)以下的人数D. 7球(不含7球)以下的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com