
����Ŀ�������ڼ�������̳�������.���̳��ķ����ǣ���һ���������������4����ȫ��ͬ��С�����Ϸֱ�ꡰ![]() Ԫ������
Ԫ������![]() Ԫ������
Ԫ������![]() Ԫ������
Ԫ������![]() Ԫ�����˿�ÿ������
Ԫ�����˿�ÿ������![]() Ԫ���Ϳɴ������ﲻ�Żص�����
Ԫ���Ϳɴ������ﲻ�Żص�����![]() ����������С��������֮�Ϳɻ���Ӧ�۸����Ʒ.���̳��ķ����ǣ���һ���������������
����������С��������֮�Ϳɻ���Ӧ�۸����Ʒ.���̳��ķ����ǣ���һ���������������![]() ����ȫ��ͬ��С�����Ϸֱ�ꡰ
����ȫ��ͬ��С�����Ϸֱ�ꡰ![]() Ԫ������
Ԫ������![]() Ԫ�����˿�ÿ������
Ԫ�����˿�ÿ������![]() Ԫ���Ϳɴ������ﲻ�Żص�����
Ԫ���Ϳɴ������ﲻ�Żص�����![]() ����������С��������֮�Ϳɻ���Ӧ�۸����Ʒ. ij�˿�������
����������С��������֮�Ϳɻ���Ӧ�۸����Ʒ. ij�˿�������![]() Ԫ��
Ԫ��
(1)���ù˿��ڼ��̳����ѣ����ٿɵü�ֵ_________Ԫ����Ʒ������ɵü�ֵ_________Ԫ����Ʒ��
(2)���û���״ͼ���б�����˵���ù˿�ȥ�ĸ��̳����ѣ������Ʒ���ܼ�ֵ������![]() Ԫ�ĸ��ʴ�.
Ԫ�ĸ��ʴ�.
���𰸡�(1)20��80��(2)ȥ���̳����ѣ���ò����ڼ�ֵ50Ԫ��Ʒ�ĸ��ʴ�.
��������
��1���������⼴����øù˿����ٿɵõĹ���ȯ������ɵõĹ���ȯ�Ľ�
��2�����ȸ��������г�����Ȼ���ɱ���������еȿ��ܵĽ����ù˿�������ȯ�Ľ�����50Ԫ������������ø��ʹ�ʽ��⼴����ô𰸣�
(1) ��������ã��ù˿����ٿɵ�0+20=20��Ԫ��������ɵ�30+50=80��Ԫ����
�ʴ�Ϊ��20��80��
(2)���ڼ��̳�����
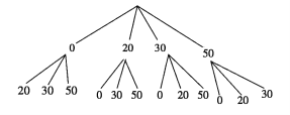
����С��������֮����12�ֵȿ��ܣ�20��30��50��20��50��70��30��50��80��50��70�����в����ڼ�ֵ50Ԫ��ռ8�֣�����![]() .
.
�������̳�����
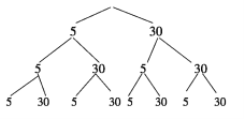
����8�ֵȿ��ܣ�15��40��40��65��40��65��65��90�����в����ڼ�ֵ50Ԫ��ռ4�֣�
����![]() .
.
��Ϊ![]() ������ȥ���̳����ѣ���ò����ڼ�ֵ50Ԫ��Ʒ�ĸ��ʴ�.
������ȥ���̳����ѣ���ò����ڼ�ֵ50Ԫ��Ʒ�ĸ��ʴ�.


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=�Cx2+1�Ķ���ΪP����A�ǵ�һ�����ڸö��κ���ͼ����һ�㣬����A��x���ƽ���߽����κ���ͼ���ڵ�B���ֱ����B��A��x��Ĵ��ߣ�����ֱ�ΪC��D������PA��PD,PD��AB�ڵ�E����PAD����PEA������ �� ��
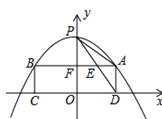
A. ʼ������B. ʼ�ղ�����C. ֻ��AB=ADʱ����D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
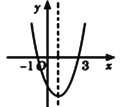
����Ŀ����ͼΪ���κ���![]() ��ͼ������˵����ȷ����____________.
��ͼ������˵����ȷ����____________.
��![]() ����
����![]() ����
����![]()
�ܵ�![]() ʱ��y��x�����������
ʱ��y��x�����������
�ݷ���![]() �ĸ���
�ĸ���![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���![]() ��ͼ����A(1��a)��B(3��a)���Ҷ����������Ϊ-4��
��ͼ����A(1��a)��B(3��a)���Ҷ����������Ϊ-4��
��1����m��n��a��ֵ��
��2���Ƕ��κ���ͼ���ڵ�A��B��IJ���ΪG (����A�͵�B)����ֱ��![]() ��ͼ��G�й����㣬��Ϻ���ͼ����k��ȡֵ��Χ��
��ͼ��G�й����㣬��Ϻ���ͼ����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
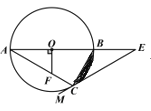
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB�ǡ�O��ֱ����OF��AB����AC�ڵ�F����E��AB���ӳ����ϣ�����EM������C���ҡ�ACE+��AFO=180��.
��1����֤��EM�ǡ�O�����ߣ�
��2������A=��E,BC=![]() ������Ӱ���ֵ����.���������
������Ӱ���ֵ����.���������![]() ���ţ�.
���ţ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ3�ġ�O�����ȱߡ�ABO�Ķ���A��B����PΪ�뾶OB�ϵĶ��㣬����AP������P��PC��AP����O�ڵ�C������ACP=30��ʱ��AP�ij�Ϊ��������
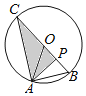
A. 3B. 3��![]() C.
C. ![]() D. 3��
D. 3��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������߾���![]() ��
��![]() ����.��
����.��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת90��õ�
��ʱ����ת90��õ�![]() ����
����![]() ����������.
����������.
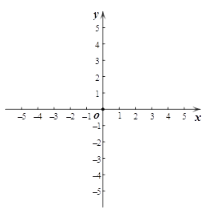
��1����������ߵı���ʽ��
��2����֪��![]() ��
��![]() ���ϣ���
���ϣ���![]() �����
�����![]() �غϣ�������
�غϣ�������![]() ����
����![]() ��
��![]() ���ƣ������
���ƣ������![]() �����ꡣ
�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
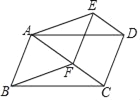
����Ŀ����ͼ��ƽ���ı���ABCD��F�ǶԽ���AC�ϵ�һ�㣬����D��DE��AC����DE��CF������AE��DE��EF��
��1����֤����ADE�ա�BCF��
��2������BAF+��AED��180�㣬��֤���ı���ABFEΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
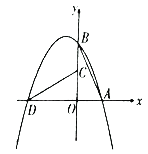
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com