
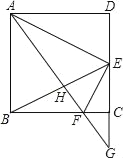
【题目】如图,正方形ABCD中,E为CD的中点,F为BC边上一点,且EF⊥AE,AF的延长线与DC的延长线交于点G,连接BE,与AF交于点H,则下列结论中不正确的是( )
A. AF=CF+BCB. AE平分∠DAF
C. tan∠CGF=![]() D. BE⊥AG
D. BE⊥AG
【答案】D
【解析】
根据E为CD的中点,且EF⊥AE,利用互余关系可证△ADE∽△ECF,由相似比可知FC:CE=DE:AD=1:2,设FC=1,则CE=DE=2,AD=AB=BC=4,根据线段的长度,勾股定理,相似三角形的判定与性质,逐一判断.
解:由E为CD的中点,设CE=DE=2,则AD=AB=BC=4,
∵EF⊥AE,
∴∠AED=90°﹣∠FEC=∠EFC,
又∵∠D=∠ECF=90°,
∴△ADE∽△ECF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得FC=1,
,解得FC=1,
A、在Rt△ABF中,BF=BC﹣FC=4﹣1=3,AB=4,由勾股定理,得AF=5,
则CF+BC=1+4=5=AF,本选项正确;
B、在Rt△ADE,Rt△CEF中,由勾股定理,得AE=2![]() ,EF=
,EF=![]() ,
,
则AE:EF=AD:DE=1:2,又∠D=∠AEF=90°,
所以,△AEF∽△ADE,∠FAE=∠DAE,即AE平分∠DAF,本选项正确;
C、∵AB∥DG,∴∠CGF=∠BAF,∴tan∠CGF=tan∠BAF=![]() =
=![]() ,本选项正确;
,本选项正确;
D、∵AB≠AE,BF≠EF,∴BE与AG不垂直,本选项错误;
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,将连续的奇数1,3,5,7…按如图中的方式排成一个数,用一个十字框框住5个数,这样框出的任意5个数中,四个分支上的数分别用a,b,c,d表示,如图所示.

(1)计算:若十字框的中间数为17,则a+b+c+d=______.
(2)发现:移动十字框,比较a+b+c+d与中间的数.猜想:十字框中a、b、c、d的和是中间的数的______;
(3)验证:设中间的数为x,写出a、b、c、d的和,验证猜想的正确性;
(4)应用:设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
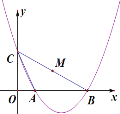
【题目】如图,抛物线![]() 交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A. n=![]() (m-
(m-![]() )2-
)2-![]() B. n=
B. n=![]() (m-
(m-![]() )2+
)2+![]()
C. n=![]() (m-
(m-![]() )2-
)2-![]() D. n=
D. n=![]() (m-
(m-![]() )2-
)2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BDcos∠HBD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次函数y=kx-6中,已知y随x的增大而减小.下列关于反比例函数y=![]()
的描述,其中正确的是( )
A. 当x>0时,y>0 B. y随x的增大而增大
C. y随x的增大而减小 D. 图像在第二、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健康的饮食习惯,为了解本校九年级学生饮食习惯,某兴趣小组在九年级随机抽取了一部分学生每天吃早餐的情况,并将统计结果绘制成如下不完整的统计图表:
组别 | 调查结果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶尔吃早餐 | 12.5% |
C | 经常吃早餐 | |
D | 每天吃早餐 | 50% |

请根据以上统计图表,解答下列问题:
![]() 本次接受调查的总人数为_____人.
本次接受调查的总人数为_____人.
![]() 请补全条形统计图.
请补全条形统计图.
![]() 该校九年级共有学生
该校九年级共有学生![]() 人,请估计该校九年级学生每天吃早餐的人数;
人,请估计该校九年级学生每天吃早餐的人数;
![]() 请根据此次调查的结果提一条建议.
请根据此次调查的结果提一条建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com