
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
【答案】C
【解析】分析:根据抛物线对称轴方程对①进行判断;由抛物线开口方向得到a<0,由对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,于是可对②进行判断;根据抛物线的对称性对③进行判断;根据顶点坐标对④进行判断;根据函数图象得当-4<x<-1时,一次函数图象在抛物线下方,则可对⑤进行判断.
详解:∵抛物线的顶点坐标A(﹣1,3),
∴抛物线的对称轴为直线x=﹣![]() =﹣1,
=﹣1,
∴2a﹣b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以②错误;
∵抛物线与x轴的一个交点为(﹣4,0)
而抛物线的对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(2,0),所以③错误;
∵抛物线的顶点坐标A(﹣1,3),
∴x=﹣1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以④正确;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(﹣1,3),B点(﹣4,0)
∴当﹣4<x<﹣1时,y2<y1,所以⑤正确.
故选:C.
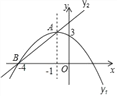
点睛:本题考查了二次函数图象与系数的关系:对于二次函数y =ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0)对称在y轴左;当a 与b异号时即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b-4ac>0时,抛物线与x轴有2个交点;△=b-4ac=0时,抛物线与x轴有1个交点;b-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将一矩形纸片ABCD沿着EF折叠,CE交AF于点G,过点G作GH∥EF,交线段BE于点H.

①判断EG与EH是否相等,并说明理由.
②判断GH是否平分∠AGE,并说明理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABC,其它条件不变.
①判断EG与EH是否相等,并说明理由.
②判断GH是否平分∠AGE,如果平分,请说明理由;如果不平分,请用等式表示∠EGH,∠AGH与∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
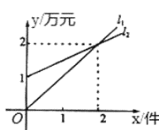
【题目】如图,![]() 表示某机床公司一天的销售收入与机床销售量的关系,
表示某机床公司一天的销售收入与机床销售量的关系,![]() 表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:①
表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:①![]() 对应的函数表达式是y=x;②
对应的函数表达式是y=x;②![]() 对应的函数表达式是y=x+1;③当销售量为2件时,销售收入等于销售成本;④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的结论为____(请把所有正确的序号填写在横线上).
对应的函数表达式是y=x+1;③当销售量为2件时,销售收入等于销售成本;④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的结论为____(请把所有正确的序号填写在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
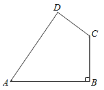
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离
的距离![]() 倍,我们就称点
倍,我们就称点![]() 是
是![]() 的巧点.若
的巧点.若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到 ![]() 的距离一半,我们就称点
的距离一半,我们就称点![]() 是
是![]() 的妙点.如图,点
的妙点.如图,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,表示
,表示![]() 的点
的点![]() 到点
到点![]() 的距离是
的距离是![]() ,到点
,到点![]() 的距离是
的距离是![]() ,那么点
,那么点![]() 是
是![]() 的巧点,点
的巧点,点![]() 是
是![]() 的妙点.
的妙点.
![]()
知识运用:
(1)如图 1,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,那么点
,那么点![]() 是(
是(![]() 的( )
的( )
![]()
A.巧点 B. 妙点 C. 无法确定
(2)如图 2,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() ,则(
,则(![]() 的巧点表示的数是 ;
的巧点表示的数是 ;
![]()

拓展提升
(3)如图 3,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() .现有一只电子蚂蚁P从点
.现有一只电子蚂蚁P从点 ![]() 出发,以每
出发,以每![]() 秒单位的速度向右运动,到达点
秒单位的速度向右运动,到达点![]() 停止. 当经过几秒时,
停止. 当经过几秒时,![]() 和
和 ![]() 其有一个点为其余两点的巧点? (请直接写出结果)
其有一个点为其余两点的巧点? (请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com