
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,我们把这条封闭曲线称为“蛋线”,已知点C的坐标为(0,-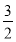 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限内是否存在一点P,使得∆PBC的面积最大?若存在,求出∆PBC面积的最大值;若不存在,请说明理由;
(3)当∆BDM为直角三角形时,请直接写出m的值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M、N两点间的距离为MN=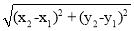 .
.
(1)A(-1,0),B(3,0);(2)存在,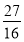 ;(3)-1或-
;(3)-1或-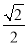 .
.
【解析】
试题分析:(1)将y=mx2-2mx-3m化为交点式,即可得到A、B两点的坐标;
(2)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到△PBC面积的最大值;
(3)先表示出DM2,BD2,MB2,再分两种情况:①DM2+BD2=MB2时;②DM2+MB2=BD2时,讨论即可求得m的值.
试题解析:(1)y=mx2-2mx-3m=m(x-3)(x+1),
∵m≠0,
∴当y=0时,x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:
 ,解得
,解得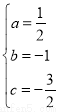 ,
,
故C1:y=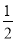 x2-x-
x2-x-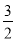 .
.
依题意,设点P的坐标为(n,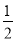 n2-n-
n2-n-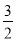 )(0<n<3)
)(0<n<3)
则S∆PBC=S∆POC+S∆BOP-S∆BOC =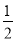 ×
×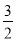 ×n+
×n+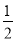 ×3×(-
×3×(-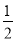 n2+n+
n2+n+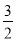 )-
)-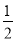 ×3×
×3×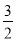
=-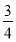 (n-
(n-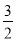 )2+
)2+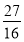
∵-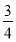 <0,
<0,
∴当n=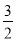 时S∆PBC的最大值是
时S∆PBC的最大值是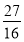
(3)y=mx2-2mx-3m=m(x-1)2-4m,顶点M坐标(1,-4m),
当x=0时,y=-3m,
∴D(0,-3m),B(3,0),
∴DM2=(0-1)2+(-3m+4m)2=m2+1,
MB2=(3-1)2+(0+4m)2=16m2+4,
BD2=(3-0)2+(0+3m)2=9m2+9,
当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.
①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,
解得m=-1(∵m<0,∴m=1舍去);
②DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,
解得m=-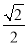 (m=
(m=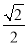 舍去).
舍去).
综上,m=-1或-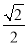 时,△BDM为直角三角形.
时,△BDM为直角三角形.
考点: 二次函数综合题.


科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,取CB的中点E,DE的延长线与AB的延长线交于点P.
(1)求证:PD是⊙O的切线;
(2)若OB=BP,AD=6,求BC的长;
(3)如图2,连接OD,AE相交于点F,若tan∠C=2,求 的值.
的值.


图1 图2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:选择题
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
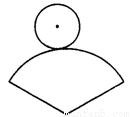
A.r B.2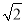 r C.
r C.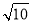 r D.3r
r D.3r
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州十五中教育集团九年级第二学期3月月考数学试卷(解析版) 题型:选择题
二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
A. B.
B. C.
C.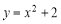 D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:解答题
在平面直角坐标系中,∆ABC的顶点坐标是A(-7,1)、B(1,1)、C(1,7),线段DE的端点坐标是D(7,-1)、E(-1,-7)
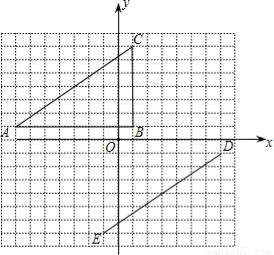
(1)试说明如何平移线段AC,使其与线段ED重合将线段AC先向______(上,下)平移_______个单位,再向_______(左,右)平移 _______个单位;
(2)将∆ABC绕坐标原点逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的∆DEF,并和∆ABC 同时绕坐标原点O逆时针旋转90o,画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:填空题
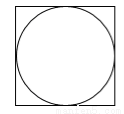
如图,在一个正方形围栏中均匀地散步者许多米粒,正方形内有一个圆(正方形的内切园),一只小鸡仔围栏内啄食,则“小鸡正在院内”啄食的概率为_______.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:解答题
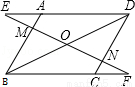
已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△ ≌△ ,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com