
如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,取CB的中点E,DE的延长线与AB的延长线交于点P.
(1)求证:PD是⊙O的切线;
(2)若OB=BP,AD=6,求BC的长;
(3)如图2,连接OD,AE相交于点F,若tan∠C=2,求 的值.
的值.


图1 图2
(1)证明见解析;
(2)BC=4;
(3)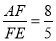 .
.
【解析】
试题分析:(1)连接BD、DO,OE,只要证明∠ODE=90°,OD是半径,就可得到DE是⊙O的切线;
(2)根据△ADB∽△BDC,从而根据相似比不难求得BD的长;
(3)根据平行线分线段成比例进行分析.
试题解析:(1)如图1,连接BD,OD,OE.

∵AB是直径,
∴∠ADB=∠CDB=90°.
∵E是BC中点,
∴DE=EC=EB,
又∵OD=OB,OE=OE,
∴△ODE≌△OBE(SSS),
∴∠ODE=∠OBE=90°,
∴OD⊥DP,
∴PD是⊙O的切线;
(2)∵OB=BP,∠ODP=90°,
∴DB=OB=BP,即DB=OB=OD.
∴△ODB是等边三角形.
∴∠DOB=60°.
∴∠A=30°,
又∵∠ABC=90°,
∴∠C=60°.
∴∠CBD=30°.
∴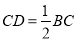 ,
,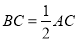 ,
,
设 ,
,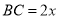 ,
,
∵AD=6,
∴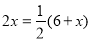 .
.
∴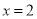 .
.
∴BC=4;
(3)如图2,连接BD,OE.

∵tan∠C=2,∠CDB=90°,
∴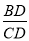 =2.
=2.
又∵∠ABD=∠C=60°,
∴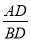 =2,
=2,
设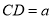 ,
, ,
,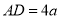 ,
,
∴AC=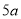 .
.
∵O是AB中点,E是BC中点,
∴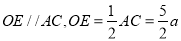 ,
,
∴ ,
,
∴ .
.
考点:圆综合题.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源:2013-2014学年湖北省黄冈市九年级下学期入学考试数学试卷(解析版) 题型:解答题
A、B两地间的距离为15千米,甲从A地出发步行前往B地,20分钟后,乙从 B地出发骑车前往A地,且乙骑车比甲步行每小时多走10千米.乙到达A地后停留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地.求甲从A地到B地步行所用的时间.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:选择题
如图,直线y=x+a-5与双曲线y=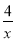 交于A,B两点,则当线段AB的长度取最小值时, a的值为( ).
交于A,B两点,则当线段AB的长度取最小值时, a的值为( ).
A.0 B.1 C.2 D.5

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
某企业向阳光小学赠送300个学生书包.现用A,B两种不同的包装箱进行包装,单独用B型包装箱比单独用A型包装箱少用10个,已知每个B型包装箱比每个A型包装箱多装5个书包.求A,B两种包装箱各能装书包多少个?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:解答题
先化简,再求代数式的值: ,其中sin230°<
,其中sin230°< <tan260°,请你取一个合适的整数作为
<tan260°,请你取一个合适的整数作为 的值代入求值.
的值代入求值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,我们把这条封闭曲线称为“蛋线”,已知点C的坐标为(0,-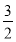 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限内是否存在一点P,使得∆PBC的面积最大?若存在,求出∆PBC面积的最大值;若不存在,请说明理由;
(3)当∆BDM为直角三角形时,请直接写出m的值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M、N两点间的距离为MN=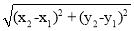 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com