
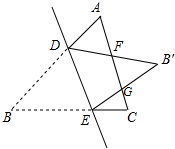
 已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′、EB′分别交边AC于点F、G,若∠ADF=75°,则∠EGC的度数为
已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′、EB′分别交边AC于点F、G,若∠ADF=75°,则∠EGC的度数为 解:如图,由题意得:
解:如图,由题意得:

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
| |ab| |
| ab |
| |ac| |
| ac |
| |bc| |
| bc |
| |abc| |
| abc |
| A、-7 | B、-1 | C、1 | D、7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
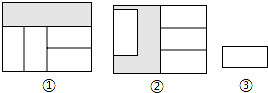 在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为a,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( )(用a的代数式表示)
在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为a,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( )(用a的代数式表示)| A、-a | ||
| B、a | ||
C、-
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )
如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )| A、AB2=AC•BD |
| B、AB•AD=BD•BC |
| C、AB2=BC•BD |
| D、AB•AD=BD•CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com