
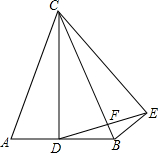
 已知AC=BC,DC=EC,∠BCA=∠DCE,CD⊥AB,求证:∠BCE=∠BEF.
已知AC=BC,DC=EC,∠BCA=∠DCE,CD⊥AB,求证:∠BCE=∠BEF. 分析 先证出∠ACD=∠BCE,由SAS证明△ACD≌△BCE,得出∠ADC=∠BEC=90°,得出∠BCE=90°-∠CBE,再证出BC⊥DE,得出∠BEF=90°-∠CBE,即可得出结论.
解答 证明:∵AC=BC,CD⊥AB,
∴∠ACD=∠BCD,∠ADC=90°,
∵∠BCA=∠DCE,
∴∠ACD=∠BCE=∠BCD,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACD=∠BCE}&{\;}\\{DC=EC}&{\;}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠ADC=∠BEC=90°,
∴∠BCE=90°-∠CBE,
∵DC=EC,∠BCE=∠BCD,
∴BC⊥DE(三线合一),
∴∠BFE=90°,
∴∠BEF=90°-∠CBE,
∴∠BCE=∠BEF.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质;熟练掌握全等三角形的判定方法和等腰三角形的性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
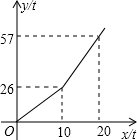 为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:
为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
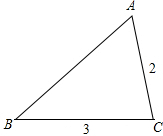 定义:如果两条线段将一个三角形分割成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图,△ABC中,AC=2,BC=3,∠C=2∠B
定义:如果两条线段将一个三角形分割成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图,△ABC中,AC=2,BC=3,∠C=2∠B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com