
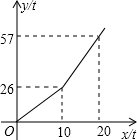
 为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:
为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:分析 (1)根据函数图象可知,用水10吨,水费为26元,即可求出a的值.
(2)由函数图象可当用水20吨时,水费为57元,b=(57-26)÷(20-10)=3.1;当x>10时,设y与x之间的函数关系式为y=kx+b,把点(10,26),(20,57)代入得到方程组,即可解答;
(3)应先判断出两家水费量的范围,再列方程组即可解答.
解答 解:(1)由函数图象可知,用水10吨,水费为26元,
∴a=26÷10=2.6;
(2)由函数图象可当用水20吨时,水费为57元,
∴b=(57-26)÷(20-10)=3.1;
当x>10时,设y与x之间的函数关系式为y=kx+b,
把点(10,26),(20,57)代入得:$\left\{\begin{array}{l}{10k+b=26}\\{20k+b=57}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=3.1}\\{b=-5}\end{array}\right.$,
∴y=3.1x-5.
(3))∵假设甲乙用水量均不超过10吨,水费不超过53元,不符合题意;
假设乙用水10吨,则甲用水14吨,
∴水费是:2.6×10+2.6×10+3.1×4=64.4>53,不符合题意;
所以甲、乙两家上月用水甲超过10吨,乙不超过10吨,
设甲、乙两家上月用水分别为x吨,y吨,
$\left\{\begin{array}{l}{x-y=4}\\{3.1x-5+2.6y=53}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=12}\\{y=8}\end{array}\right.$,
甲、乙两家上月用水分别为12吨,8吨.
点评 本题主要考查了一次函数与图形的结合,解决本题的关键是应注意分段函数的计算方法.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
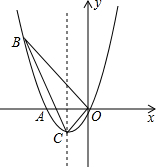 已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C
已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com