练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．先化简，再求值：[（x+y）（x-y）-（x-y）2]÷2y，其中x=-$\frac{1}{2}$，y=$\frac{1}{3}$．

    分析 先算乘法，再合并同类项，算除法，最后代入求出即可．

    解答 解：[（x+y）（x-y）-（x-y）2]÷2y
    =[x2-y2-x2+2xy-y2]÷2y
    =（-2y2+2xy）÷2y
    =-y+x，
    当x=-$\frac{1}{2}$，y=$\frac{1}{3}$时，原式=-$\frac{1}{3}$-$\frac{1}{2}$=-$\frac{5}{6}$．

    点评 本题考查了整式的混合运算和求值的应用，能运用整式的运算法则进行化简是解此题的关键，难度适中．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．中新网2014年11月19日电 据财政部网站消息，为保证城乡义务教育阶段学校春季开学后正常运转和“两免一补”政策落实到位，中央财政下达2015年城乡义务教育补助经费部分预算697.2亿元．将697.2亿用科学记数法表示应为（　　）
    A．6.972×1011B．6.972×1010C．0.6972×103D．6.972×102

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图①，在平面直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别落在x，y轴上，且OA=8，OC=4．
    （1）直接写出点A，B，C的坐标；
    （2）如图②，把矩形OABC沿对角线AC折叠，使点B落在点D处，且CD交x轴于点E，连结OD，那么下列说法中正确的有①②③
    ①△EDA≌△EOC；②∠ECA=∠EAC；③OD∥AC；④△COD是等腰三角形；⑤CD平分∠ACO
    （3）求出图②中点E坐标；
    （4）计算说四边形ODAC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．在关系式y=3x-1中，当x由1变化到5时，y由2变化到14．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，已知OC⊥AB，如果∠BOD=30°，则∠COD的度数为60°．

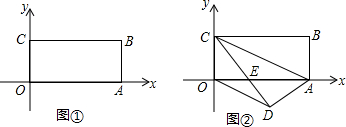
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．“扬州是我家，爱护靠大家”．自我市开展整治“六乱”行动以来，我市学生更加自觉遵守交通规则．某校学生小明每天骑自行车上学时都要经过一个十字路口，该十字路口有红、黄、绿三色交通信号灯，他在路口遇到红灯的概率为$\frac{1}{3}$，遇到黄灯的概率为$\frac{1}{9}$，那么他遇到绿灯的概率为（　　）
    A．$\frac{2}{3}$B．$\frac{1}{3}$C．$\frac{4}{9}$D．$\frac{5}{9}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

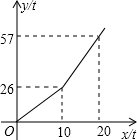    8．为鼓励节约用水，某市自来水公司对居民用水采用以户为单位分段计费办法收费，即一个月用水10t以内（包含10t）的用户，收水费a元/t，一月用水超过10t的用户，按b元/t（b＞a）收费，设一户居民用水x t，应收水费y元，y与x之间的函数关系式如图所示：
    （1）求a的值；
    （2）求b的值，并写出当x＞10时，y与x之间的函数关系式；
    （3）已知居民甲上月比居民乙多用水4t，两家共收水费53元，求他们上月分别用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，AC=BC，DC=EC，且AC⊥BC，DC⊥EC．求证：
    （1）AE=BD；
    （2）AE⊥BD；
    （3）∠AEC=∠BDC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（1）计算：（-2）2+（$\sqrt{3}$-π）0+|1-$\sqrt{3}$|；
    （2）解方程组：$\left\{\begin{array}{l}{2x+y=1}\\{x-2y=3}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案