Question

【题目】如图，已知抛物线y=﹣ x2+bx+c与x轴相交于点A，B（4，0），与y轴相交于点C，直线y=﹣x+3经过点C，与x轴相交于点D．

（1）求抛物线的解析式；
（2）点P为第一象限抛物线上一点，过点P作x轴的垂线，垂足为点E，PE与线段CD相交于点G，过点G作y轴的垂线，垂足为点F，连接EF，过点G作EF的垂线，与y轴相交于点M，连接ME，MD，设△MDE的面积为S，点P的横坐标为t，求S与t的函数关系式；
（3）在（2）的条件下，过点B作直线GM的垂线，垂足为点K，若BK=OD，求：t值及点P到抛物线对称轴的距离．

Answer 1

【答案】
（1）

解：对于直线y=﹣x+3，令x=0得y=3，

∴C（0，3），把B（4，0），C（0，3）的坐标代入y=﹣ x2+bx+c得 ，解得 ，

∴抛物线的解析式为y=﹣ x2+ x+3

（2）

解：如图1中，当0＜t＜ 时，P（t，﹣ t+ t+3），

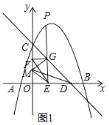
∵FG⊥OC，GE⊥OD，CO⊥OD，

∴四边形FOGE是矩形，

∴OE=FG=t，GE=GD=3﹣t，

∵MG⊥FE，FG⊥GE，

∴∠GEF+∠GFE=90°，∠GFE+∠FGM=90°，

∴∠GEF=∠FGM，

在Rt△FGE中，tan∠FEG= = ，

∴在Rt△FGM中，tan∠FGM= = ，

∴FM= ，

∴OM=FO﹣FM=（3﹣t）﹣ = ，

∴S= DEOM= ×（3﹣t）× = ，

当 ＜t＜3时，S= DEOM= DE（FM﹣OF）= ．

综上所述，S=

（3）

解：如图2中，过点C作x轴的平行线，过点B作y轴的平行线，两直线交于点Q，延长MK与CQ交于点N，延长KM与x轴交于点Z，

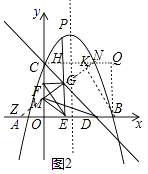
∵CQ∥BO，BQ∥CO，

∴四边形COBQ是平行四边形，

∵∠COB=90°，

∴四边形COBQ是矩形，

∴∠CQB=90°=∠BKN，CO=BQ=3，

对于直线y=﹣x+3，令y=0得x=3，

∴D（0，3），

∴OD=OC=BQ=3，

∵BK=OD，

∴BK=BQ，∵BN=BN，

∴Rt△KBN≌Rt△QBN，

∴∠KNB=∠QNB，

∵NQ∥OB，

∴∠QNB=∠NBO=∠KNB，

∴ZN=ZB，设EG交CQ于H，

∵OC=OB，

∴∠OCD=∠ODC，

∵CQ∥OB，

∴∠QHG=∠HEO=90°，∠HCD=∠CDO，

∴∠OCD=∠HCD，

∵GF⊥OC，GH⊥CH，

∴GH=GF，

∵GM⊥EF，GH⊥HN，

∴∠GEM+∠MGE=90°，∠HGN+∠HNG=90°，

∵∠HGN=∠MGE，

∴∠GEM=∠HNG，

∵∠GFO=∠FOE=∠OEG=90°，

∴∠GEF=90°=∠GHN，

∴△HNG≌△FGE，

∴CH=OE=t=GH，HN=GE=3﹣t，

∴CN=3﹣t+3=3，

∴NQ=BD=1=NK，设ZK=m，则ZB=ZN=m+1，

在Rt△KZB中，（m+1）2=m2+32，

∴m=4，

∴ZB=5，

∴tan∠GZB= ，tan∠GEF= ，

∴ = ，

∴t= ，

∵抛物线的对称轴x= ，

∴点P到抛物线的对称轴的距离为 ﹣ =

【解析】（1）求出点C坐标，利用待定系数法转化为方程组解决问题．（2）分两种情形①当0＜t＜ 时，P（t，﹣ t+ t+3），②当 ＜t＜3时，分别求出OM的长即可解决问题．（3）如图2中，过点C作x轴的平行线，过点B作y轴的平行线，两直线交于点Q，延长MK与CQ交于点N，延长KM与x轴交于点Z，Rt△KBN≌Rt△QBN，推出∠KNB=∠QNB，由NQ∥OB，推出∠QNB=∠NBO=∠KNB，推出ZN=ZB，设EG交CQ于H，由△HNG≌△FGE，推出CH=OE=t=GH，HN=GE=3﹣t，推出CN=3﹣t+3=3，推出NQ=BD=1=NK，设ZK=m，则ZB=ZN=m+1，在Rt△KZB中，（m+1）2=m2+32 ， 推出m=4，推出ZB=5，于tan∠GZB= ，tan∠GEF= ，可得 = ，求出t即可解决问题．