

分析 (1)先求出CP=1,利用对称得出∠MBN=90°,BP=BP=3,最后用锐角三角函数的定义即可;
(2)先求出FG,再利用同角的三角函数相等,得出PG,再用三角形的面积公式求解即可;
(3)利用对称先判断出AM=AP=AN,进而得出三角形AMN是等腰直角三角形,即可得出∠AMN=45°,得出∠AFE=∠AMB,即可判断出△AEF∽△BAM.
解答  解:(1)如图1,连接BN,
解:(1)如图1,连接BN,
∵点P为边BC的中点,
∴CP=BP=$\frac{1}{2}$BC=1,
∵点P与点M关于AC对称,
∴CM=CP=1
∵∠ACB=90°,AC=BC=2,
∴∠BAC=∠ABC=45°,
∵点P与点N关于AB对称,
∴BP=BN=1,∠ABN=∠ABC=45°,
∴∠CBM=90°,BM=CM+BC=3
在Rt△MBN中,tan∠M=$\frac{BN}{BM}$=$\frac{1}{3}$;
(2)如图2,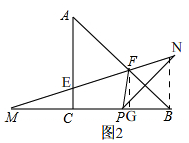 过点F作FG⊥BC,
过点F作FG⊥BC,
设PG=m,
∴BG=BP-PG=2-x-m,MG=MP+PG=2x+m,
在Rt△BFG中,∠FBG=45°,
∴FG=BG=2-x-m,
在Rt△FMG中,tan∠M=$\frac{FG}{MG}$=$\frac{2-x-m}{2x+m}$,
在Rt△MNB中,tan∠M=$\frac{BN}{BM}$=$\frac{2-x}{2+x}$,
∴$\frac{2-x-m}{2x+m}=\frac{2-x}{2+x}$,
∴m=$\frac{(x-2)^{2}}{4}$,
∴FG=2-x-$\frac{(x-2)^{2}}{4}$
∴y=S△MPF=$\frac{1}{2}$MP•FG=$\frac{1}{2}$×2x×[2-x-$\frac{(x-2)^{2}}{4}$]=$\frac{x(2-x)(2+x)}{4}$(0<x<2);
(3)△AEF∽△BAM
理由:如图3, 连接AM,AP,AN,BN,
连接AM,AP,AN,BN,
∵点P关于直线AC、AB的对称点分别为M、N,
∴AM=AP=AN.∠MAC=∠PAC,∠PAB=∠NAB,
∵∠BAC=∠PAC+∠PAB=45°,
∴∠MAN=∠MAC+∠PAC+∠BAP+∠NAB=2(∠PAC+∠PAB)=90°,
∴∠AMN=45°=∠ABC,
∵∠AFE=∠ABC+∠BMF,∠AMB=∠AMN+∠BMF,
∴∠AFE=∠AMB,∵∠EAF=∠ABM=45°,
∴△AEF∽△BAM.
点评 此题是相似形综合题,主要考查了锐角三角函数,勾股定理,对称的性质,三角形的面积公式,相似三角形的判定和性质,解本题的关键是得出△PFM的边PM上高和△MAN是等腰直角三角形,是一道很好的中考常考题.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D在∠ACB的平分线上,过点D作BC的平行线与∠ACB的外角平分线相交于点E,DE交AC于点F
如图,在△ABC中,点D在∠ACB的平分线上,过点D作BC的平行线与∠ACB的外角平分线相交于点E,DE交AC于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
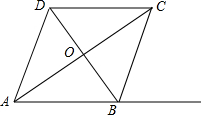 已知:如图,菱形ABCD周长为20,对角线AC、BD交于点O,sin∠BAC=$\frac{3}{5}$.
已知:如图,菱形ABCD周长为20,对角线AC、BD交于点O,sin∠BAC=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
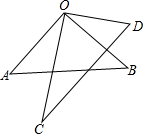 如图,∠AOB=∠COD=90°,
如图,∠AOB=∠COD=90°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒.
如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com