
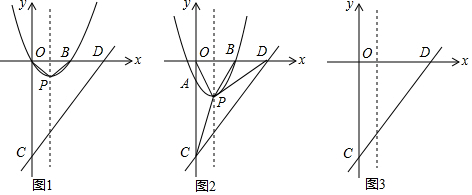
���� ��1�������������ϵ�����������������߶��㹫ʽ���ɵó�B��P���꣬�����ù��ɶ������涨�����ɵó����ۣ�
��2����ȷ������C��D���꣬�����M�����꣬ȷ����ƽ�ƺ������ߵĶ������꣬�����ó�PM�����ɵó���PCD�������
�������POC��������ɵó���PCD�����������������ʽ����ȷ������P���ꣻ
�������POD��������������������Ѱ�ҡ�PCD�͡�POD�������ϵ��
��� �⣺��1����������y=x2-2x=x��x-2����
��B��2��0����
��������y=x2-2x=��x-1��2-1��
��P��1��-2����
��OP2=2��BP2=2OB2=4��
��OP2+BP2=OB2��OP=BP��
���OBP�ǵ���ֱ�������Σ�
�ʴ�Ϊ����2��0������OBP�ǵ���ֱ�������Σ�
��2����ͼ2��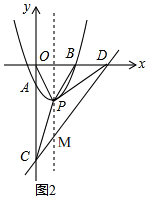 ��ֱ��y=x-4��y�ύ�ڵ�C����x�ύ�ڵ�D��
��ֱ��y=x-4��y�ύ�ڵ�C����x�ύ�ڵ�D��
��C��0��-4����D��4��0����
��x=1ʱ��y=-3��
��M��1��-3����
����������ƽ��m����λ���ȣ�
��ƽ�ƺ�������߽���ʽΪy=��x-1��2-��1+m����P��1��-��1+m����
��PM=|-��1+m��+3|=|m-2|
��S��PCD=S��PMC+S��PMD=$\frac{1}{2}$PM•|xD-xC|=$\frac{1}{2}$��|m-2|��4=2|m-2|��
��S��POC=$\frac{1}{2}$AC��|xP|=$\frac{1}{2}$��4��1=2��
��S��PCD=$\sqrt{2}$S��POC��
��S��PCD=2|m-2|=2$\sqrt{2}$��
��m=2+$\sqrt{2}$��m=2-$\sqrt{2}$��
��P��1��-��3+$\sqrt{2}$������1��-��3-$\sqrt{2}$������
��S��POD=$\frac{1}{2}$OD•|yP|=$\frac{1}{2}$��4��|-��1+m��|=2|m+1|
��m��2ʱ��
��S��PCD=2|m-2|=2m-4
S��POD=2|m+1|=2m+2��
��S��POD-S��PCD=6��
��-1��m��2ʱ��
��S��PCD=2|m-2|=4-2m
S��POD=2|m+1|=2m+2��
��S��POD+S��PCD=6��
��m��-1ʱ��
��S��PCD=2|m-2|=4-2m
S��POD=2|m+1|=-2-2m��
��S��PCD-S��POD=6��
������m��2ʱ��S��POD-S��PCD=6����-1��m��2ʱ��S��POD+S��PCD=6����m��-1ʱ��S��PCD-S��POD=6��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�������������ϵ���ص㣬ֱ�������ε��ж��������ε������ʽ�������ֵ���̣�������������ϵ������������ļ��㷽���ǽⱾ��Ĺؼ������ò���Ѱ�ҡ�POD�͡�PCD�������ϵ�ǽⱾ����ѵ㣬��һ���е��ѵ���п������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��GΪBC���е㣬��DG��BC��DE��AB��E��DF��AC��F��BE=CF��
��ͼ��GΪBC���е㣬��DG��BC��DE��AB��E��DF��AC��F��BE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
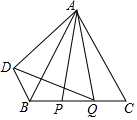 ��ͼ����ABC�ǵȱ������Σ�AB=2cm������P��Q�ֱ�ӵ�B��Cͬʱ�������˶��ٶȾ�Ϊ2cm/s����P��B���������B��C�˶�������Cֹͣ����Q�ӵ�C��������C��B�˶�������Bֹͣ������AP��AQ����P����ֱ��AB�ĶԳƵ�ΪD������BD��DQ�����P���˶�ʱ��Ϊt��s����
��ͼ����ABC�ǵȱ������Σ�AB=2cm������P��Q�ֱ�ӵ�B��Cͬʱ�������˶��ٶȾ�Ϊ2cm/s����P��B���������B��C�˶�������Cֹͣ����Q�ӵ�C��������C��B�˶�������Bֹͣ������AP��AQ����P����ֱ��AB�ĶԳƵ�ΪD������BD��DQ�����P���˶�ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���C=90�㣬sinB=$\frac{3}{5}$��AB=15�����ABC���ܳ���tanA��ֵ��
��ͼ���ڡ�ABC�У���C=90�㣬sinB=$\frac{3}{5}$��AB=15�����ABC���ܳ���tanA��ֵ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com