

���� ��1���������A��B�����꣬��CΪOB���е㣬C�����꣬EΪAB���е㣬�����CEΪ��OAB����λ�ߣ��ó�CE=$\frac{1}{2}$OA=$\frac{1}{2}$CD=3�����ɣ�
��2���ٷֵ�P��OA��OC�ϣ���������IJ�ɵó����ۣ�
�ڷ������������0��t��3ʱ��������ó�����t�ķ��̣��ⷽ�̼��ɣ�
��t=3ʱ���ɡ�EOC�����=$\frac{1}{2}$��3��4=6��18��$\frac{1}{4}$���ó�t��3��
��3��t��5ʱ��Qֹͣ�˶���OP=2t-6���ó�CP=10-2t���ɡ�ECP�����=$\frac{1}{2}$��3����10-2t��=$\frac{1}{4}$��18���ⷽ�̼��ɣ�
��� ��1��֤��������ֱ��y=$\frac{4}{3}$x+8��
��x=0ʱ��y=8����y=0ʱ��x=-6��
��A��-6��0����B��0��8����OA=6��OB=8��
���ı���AOCD�Ǿ��Σ�
��OA��CD��CD=OA=6��AD=OC=4��
��D��-6��4����
�ߵ�CΪOB���е㣬
��EΪAB���е㣬
��CEΪ��OAB����λ�ߣ�
��CE=$\frac{1}{2}$OA=$\frac{1}{2}$CD=3��
��E��-3��4��
�ʴ�Ϊ����-6��4������-3��4��
��2���⣺�ٵ�0��t��3ʱ����ͼ3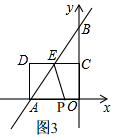
���˶�֪��AP=2t��
��S=S��PAE=$\frac{1}{2}$AP��OC=2��2t=4t��
��3��t��5ʱ����ͼ4��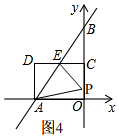
���˶�֪��OP=2t-OA=2t-6����OC=4����PC=OC-OP=4-��2t-6��=10-2t��
��S=S��PAE=S����AOCE-S��AOP-S��PCE
=$\frac{1}{2}$��CE+OA��•OC-$\frac{1}{2}$OA•OP-$\frac{1}{2}$CE•PC
=$\frac{1}{2}$��3+6����4-$\frac{1}{2}$��6����2t-6��-$\frac{1}{2}$��3����10-2t��
=-3t+21
��S=$\left\{\begin{array}{l}{4t��0��t��3��}\\{-3t+21��3��t��5��}\end{array}\right.$
�ڴ��ڣ�
����AOCE�����=$\frac{1}{2}$��3+6����4=18��
������������ۣ�
��0��t��3ʱ����ͼ1��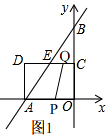
������APQE�����=$\frac{1}{2}$��2t+3-t����4=18��$\frac{1}{4}$��
��ã�t=-$\frac{3}{4}$���������⣬��ȥ��
������APQE�����=$\frac{1}{2}$��2t+3-t����4=18��$\frac{3}{4}$��
��ã�t=$\frac{15}{4}$���������⣬��ȥ��
��t=3ʱ���ߡ�EOC�����=$\frac{1}{2}$��3��4=6��18��$\frac{1}{4}$��
��t��3��
��3��t��5ʱ����ͼ2��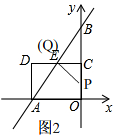
Qֹͣ�˶�����Q��E�غϣ���OP=2t-6��
��CP=4-��2t-6��=10-2t��
����ECP�����=$\frac{1}{2}$��3����10-2t��=$\frac{1}{4}$��18ʱ��
��ã�t=$\frac{7}{2}$���������⣻
������������t=$\frac{7}{2}$ʱ��ֱ��PQ���ı���AOCE������ֳ�1��3������
���� ������һ�κ����ۺ��⣬������һ�κ������������������������λ�ߵ����ʡ���������ļ��㡢����������ļ��㡢�ⷽ�̵�֪ʶ�������ѶȽϴ��ۺ���ǿ���ر��ǣ�2���У���Ҫ���з������ۣ����ܵó������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 83��104 | B�� | 8.3��104 | C�� | 8.3��105 | D�� | 0.83��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���D�ڡ�ACB��ƽ�����ϣ�����D��BC��ƽ�������ACB�����ƽ�����ཻ�ڵ�E��DE��AC�ڵ�F
��ͼ���ڡ�ABC�У���D�ڡ�ACB��ƽ�����ϣ�����D��BC��ƽ�������ACB�����ƽ�����ཻ�ڵ�E��DE��AC�ڵ�F�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
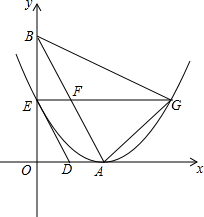 ��ͼ��ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��x�ᡢx��ֱ��ڵ�A��B��������D��E�ֱ��A��Bͬʱ�������O�˶����˶���O��ֹͣ�����˶��ٶȷֱ���1����λ����/���$\sqrt{3}$����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������ΪG�㣬��AB�ཻ�ڵ�F��
��ͼ��ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��x�ᡢx��ֱ��ڵ�A��B��������D��E�ֱ��A��Bͬʱ�������O�˶����˶���O��ֹͣ�����˶��ٶȷֱ���1����λ����/���$\sqrt{3}$����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������ΪG�㣬��AB�ཻ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�ڽ��ڡ�O��BD�ǡ�O��ֱ����AE��CD������ΪE��DAƽ�֡�BDE��
��ͼ���ı���ABCD�ڽ��ڡ�O��BD�ǡ�O��ֱ����AE��CD������ΪE��DAƽ�֡�BDE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
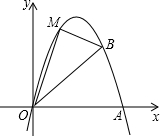 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��5��0����B��4��4��
��ͼ����ƽ��ֱ������ϵ�У���֪��A��5��0����B��4��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
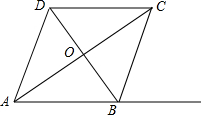 ��֪����ͼ������ABCD�ܳ�Ϊ20���Խ���AC��BD���ڵ�O��sin��BAC=$\frac{3}{5}$��
��֪����ͼ������ABCD�ܳ�Ϊ20���Խ���AC��BD���ڵ�O��sin��BAC=$\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com