
分析 设原来有x个桃子,因为第一只猴子朝海里扔了一个,正好可以分成5堆,所以我们借给猴子4个桃子,那么正好可以分成5堆,第一个猴子就拿了其中一份(包括它吃掉的一个),但是,它并没有多得桃子,就是(x+4)×$\frac{1}{5}$=(x-1)×$\frac{1}{5}$+1,同理,第三,第四和第五;最后,剩下的桃子是(x+4)×$\frac{4}{5}$×$\frac{4}{5}$×$\frac{4}{5}$×$\frac{4}{5}$×$\frac{4}{5}$=(x+4)×($\frac{4}{5}$)5,这应该是个整数,进而得出(x+4)一定要能被55=3125整除,求出即可.
解答 解:设原来有x个桃子,因为第一只猴子朝海里扔了一个,恰好可以分成5份,
所以我们借给猴子4个桃子,那么正好可以分成5堆,第一个猴子就拿了其中一份(包括它吃掉的一个),
但是,它并没有多得桃子,就是(x+4)×$\frac{1}{5}$=(x-1)×$\frac{1}{5}$+1,
因为它没有多得,所以剩下的桃子比原来剩下的多4个.
那么剩下的桃子同理也恰好可以分成5份,第二只猴子又拿走了一份(同样,包括它吃掉的一个),
同理,第三,第四和第五;
最后,剩下的桃子是(x+4)×$\frac{4}{5}$×$\frac{4}{5}$×$\frac{4}{5}$×$\frac{4}{5}$×$\frac{4}{5}$=(x+4)×($\frac{4}{5}$)5,
这应该是个整数,
所以,(x+4)一定要能被55=3125整除,
所以x+4最小是3125,此时,x为3121,
即:原来发现的桃子至少有3121个.
点评 此题是应用类问题应用,属于逆向推理问题,考查学生能够运用所学知识推断一些简单的逻辑问题的能力,整除问题;审清题意,列出代数式是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}-{b}^{2}}{a-b}$=a-b | B. | $\frac{y+a}{x+a}$=$\frac{y}{x}$ | C. | $\frac{m-n}{n-m}$=-1 | D. | $\frac{-a-b}{a-b}$=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50=0 | B. | 2-3=$\frac{1}{6}$ | C. | ($\frac{1}{3}$)-1<(-3)0<(-3)-2 | D. | (-3)-2<(-3)0<($\frac{1}{3}$)-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 83×104 | B. | 8.3×104 | C. | 8.3×105 | D. | 0.83×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,点D是△ABC中BC边上一点,点E是AD上任意一点,且EB=EC,∠ABE=∠ACE.
已知:如图,点D是△ABC中BC边上一点,点E是AD上任意一点,且EB=EC,∠ABE=∠ACE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D在∠ACB的平分线上,过点D作BC的平行线与∠ACB的外角平分线相交于点E,DE交AC于点F
如图,在△ABC中,点D在∠ACB的平分线上,过点D作BC的平行线与∠ACB的外角平分线相交于点E,DE交AC于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
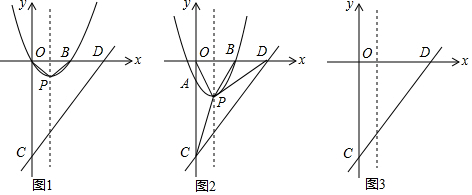
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com