
 已知:如图,△ABC内接于⊙O,AD为⊙O的弦,∠1=∠2,DE⊥AB于E,DF⊥AC于F.求证:BE=CF.
已知:如图,△ABC内接于⊙O,AD为⊙O的弦,∠1=∠2,DE⊥AB于E,DF⊥AC于F.求证:BE=CF. 分析 连接DB、DF,然后根据角平分线的性质可以得到DE和DF的关系,弦DB和DC的关系,再根据三角形全等的知识可以得到BE和CF的关系.
解答 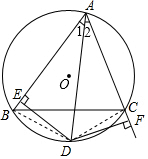 证明:连接DB、DF,
证明:连接DB、DF,
∵∠A的平分线AD交圆于D,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DFB=∠DFC=90°,∠BAD=∠CAD,
∴DB=DC,
∴在Rt△BED和Rt△CFD中,$\left\{\begin{array}{l}{DE=DF}\\{DB=DC}\end{array}\right.$
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
点评 本题考查圆周角定理、全等三角形的判定和性质、角平分线的性质,解题的关键是明确题意,找出所求问题需要的条件.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:选择题
| A. | 实际每天铺设管道的长度 | B. | 实际施工的天数 | ||
| C. | 原计划施工的天数 | D. | 原计划每天铺设管道的长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+3y)(x-3y)=x2-9y2 | B. | a(x+y+1)=ax+ay+a | ||
| C. | 4x2-1=(2x+1)(2x-1) | D. | a2c-a2b+1=a2(c-b)+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
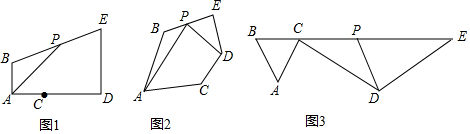
 如图,四边形ABCD是正方形,点E为ABCD内一点,将BE绕点B顺时针旋转90°得到BF,连接EF、AE、CF,EF与CB交于点G.
如图,四边形ABCD是正方形,点E为ABCD内一点,将BE绕点B顺时针旋转90°得到BF,连接EF、AE、CF,EF与CB交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,G为BC的中点,且DG⊥BC,DE⊥AB于E,DF⊥AC于F,BE=CF.
如图,G为BC的中点,且DG⊥BC,DE⊥AB于E,DF⊥AC于F,BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
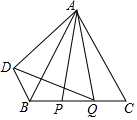 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com