
【题目】某商场服装部销售一种名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价
元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价![]() 元时,平均每天可多卖出
元时,平均每天可多卖出![]() 件.
件.
(1)若商场要求该服装部每天盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
【答案】(1)设每件应降价x元,由题意可列方程为(40-x)(30+2x)=1200,
解得x1=0,x2=25,
当x=0时,能卖出30件;
当x=25时,能卖出80件.
根据题意,x=25时能卖出80件,符合题意,不降价也能盈利1200元,符合题意.
因为要减少库存,所以应降价25元.
答:每件衬衫应降价25元;
(2)设商场每天盈利为W元.
W=(40-x)(30+2x)
=-2x2+50x+1200
=-2(x2-25x)+1200
=-2(x-12.5)2+1512.5.
当每件衬衫降价为12或13元时,商场服装部每天盈利最多.
【解析】
(1)本题的关键语“每件降价1元时,平均每天可多卖出2件”,设每件应降价x元,用x来表示出商场所要求的每件盈利的数额量,然后根据盈利1200元来列出方程;
(2)根据(1)中的方程,然后按一元二次方程的特点,来求出最大值.
解:(1)设每件应降价x元,由题意可列方程为(40-x)·(30+2x)=1200,
解得x1=0,x2=25,
当x=0时,能卖出30件;
当x=25时,能卖出80件.
根据题意,x=25时能卖出80件,符合题意.
故每件衬衫应降价25元.
(2)设商场每天盈利为W元.
W=(40-x)(30+2x)=-2x2+50x+1200=-2(x2-25x)+1200=-2(x-12.5)2+1512.5
当每件衬衫降价为12.5元时,商场服装部每天盈利最多,为1512.5元.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五.它被记载于我国古代著名数学著作《周髀算经》中,在本题中,我们把三边的比为3∶4∶5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
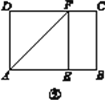
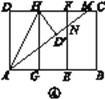
实践操作 如图①,在矩形纸片ABCD中,AD=8 cm,AB=12 cm.
第一步:如图②,将图①中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图④,将图③中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图②中证明四边形AEFD是正方形;
(2)请在图④中判断NF与ND′的数量关系,并加以证明;
(3)请在图④中证明△AEN是(3,4,5)型三角形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将一副三角板(直角三角板![]() 和直角三角板
和直角三角板![]() )的两个顶点重合于点
)的两个顶点重合于点![]() .
.
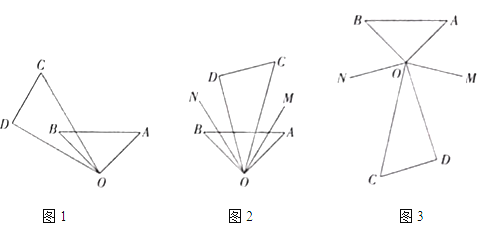
(1)如图1,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,当
逆时针方向转动,当![]() 恰好平分
恰好平分![]() 时,
时,![]() 的度数是 _.
的度数是 _.
(2)如图2,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,如果三角板
,如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
(3)当三角板![]() 绕点
绕点![]() 继续转动到如图3所示的位置时,作射线
继续转动到如图3所示的位置时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,请你求出此时钝角
,请你求出此时钝角![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个) | 售价(元/个) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于整式![]() (其中m是大于
(其中m是大于![]() 的整数).
的整数).
(1)若![]() ,且该整式是关于x的三次三项式,求m的值;
,且该整式是关于x的三次三项式,求m的值;
(2)若该整式是关于x的二次单项式,求m,n的值;
(3)若该整式是关于x的二次二项式,则m,n要满足什么条件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com