
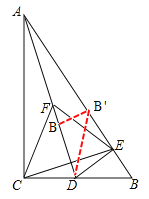
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.

【答案】(1)等边三角形,理由见解析(2) n=60°或135°.
【解析】
(1)根据直角三角形斜边的中线等于斜边的一半证得FC=FE即可,再证明∠CFE=60°,从而进行判断;
(2)根据∠B=60°,∠DEB=90°,可知BD=![]() DE,又BD=
DE,又BD=![]() CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠BDB'等于旋转角,分两种情况求解即可..
CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠BDB'等于旋转角,分两种情况求解即可..
(1)∵∠ACB=90°,F是AD中点,
∴FC=![]() AD,
AD,
∵DE⊥AB,F是AD中点,
∴EF=![]() AD,
AD,
∴FC=FE,
∴△CEF是等腰三角形;
又EF=AF,CF=AF,故∠CFE=2∠CAB=60°
从而可知:△CEF是等边三角形.
(2)n=60°或135°
理由:①将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边AC上时,此时记为B'点,

△B'CD为直角三角形,
又∵BD=![]() CD,
CD,
故∠B'DC=45°;从而旋转角∠BDB'=180°-∠B'DC=180°-45°=135°
②当B'在边AB上时,有DB=DB',又∠B=60°,故可知△DBB'为等边三角形,所以∠BDB'=60°;即n=60°


科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部销售一种名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价
元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价![]() 元时,平均每天可多卖出
元时,平均每天可多卖出![]() 件.
件.
(1)若商场要求该服装部每天盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程a2x2+(2a-1)x+1=0有两个不相等的实数根x1,x2.
(1)求a的取值范围;
(2)是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
解:(1)根据题意,得Δ=(2a-1)2-4a2>0,解得a<![]() .∴当a<0时,方程有两个不相等的实数根. (2)存在.理由如下:如果方程的两个实数根x1,x2互为相反数,则x1+x2=-
.∴当a<0时,方程有两个不相等的实数根. (2)存在.理由如下:如果方程的两个实数根x1,x2互为相反数,则x1+x2=-![]() =0,① 解得a=
=0,① 解得a=![]() ,经检验,a=
,经检验,a=![]() 是方程①的根.∴当a=
是方程①的根.∴当a=![]() 时,方程的两个实数根x1与x2互为相反数.上述解答过程是否有错误?如果有,请指出错误之处,并解答.
时,方程的两个实数根x1与x2互为相反数.上述解答过程是否有错误?如果有,请指出错误之处,并解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
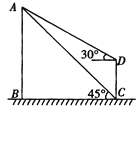
【题目】为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( )
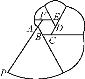
A. 13π cm B. 14π cm C. 15π cm D. 16π cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com