
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线一点,点
延长线一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() .
.
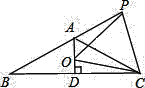
(1)已知![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() 是等边三角形;
是等边三角形;
(3)求证:![]() .
.
【答案】(1)12°;(2)证明见详解;(3)证明见详解.
【解析】
(1)连接OB,根据等腰三角形的性质可得OB=OC,再利用等边对等角可得∠APO=∠ABO,∠OBD=∠OCD,则∠APO+∠OCD=∠ABO+∠OBD=∠ABD,据此即可求解;
(2)证明∠POC =60°且OP=OC,即可证明![]() 是等边三角形;
是等边三角形;
(3)先证明∠APO=∠CPE,利用SAS即可证明![]() ,则AO=CE,即AC=AE+CE=AO+AP.
,则AO=CE,即AC=AE+CE=AO+AP.
(1)如图所示,连接OB,
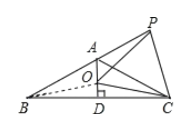
∵![]() ,
,![]() ,
,![]() ,
,
∴BD=CD,∠BAD=![]() ∠BAC=60°,
∠BAC=60°,
∴OB=OC,∠ABC=30°,
∵OP=OC,
∴OP=OC=OB,
∴∠APO=∠ABO,∠OBD=∠OCD,
∴∠APO+∠OCD=∠ABO+∠OBD=∠ABD,
∵∠ABD=30°,∠APO=18°,
∴∠DCO=∠ABD-∠APO=30°-18°=12°;
(2)∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-∠OPC-∠OCP=60°,
∵OP=OC,
∴![]() 是等边三角形;
是等边三角形;
(3)如图所示,在AC上截取AE=PA,连接PE,
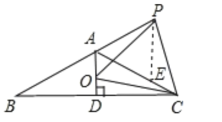
∵∠PAE=180°-∠BAC=60°,
∴![]() 是等边三角形,
是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
又∵OP=CP,PA=PE,
∴![]() (SAS),
(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD 为△ABC 的高线,AD=BC,以 AB 为底边作等腰 Rt△ABE,连接 ED, EC,延长CE 交AD 于F 点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )

A. ①③B. ①②④C. ①②③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将一副三角板(直角三角板![]() 和直角三角板
和直角三角板![]() )的两个顶点重合于点
)的两个顶点重合于点![]() .
.
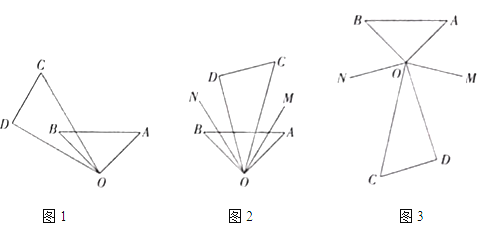
(1)如图1,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,当
逆时针方向转动,当![]() 恰好平分
恰好平分![]() 时,
时,![]() 的度数是 _.
的度数是 _.
(2)如图2,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,如果三角板
,如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
(3)当三角板![]() 绕点
绕点![]() 继续转动到如图3所示的位置时,作射线
继续转动到如图3所示的位置时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,请你求出此时钝角
,请你求出此时钝角![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
![]()
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16 cm,水面最深地方的高度为4 cm,求这个圆形截面的半径;
(3)在(2)的条件下,小明把一只宽12 cm的方形小木船放在修好后的圆柱形水管里,已知船高出水面13 cm,问此小船能顺利通过这个管道吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个) | 售价(元/个) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 中心在原点,且顶点
中心在原点,且顶点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 分别从点
分别从点![]() 同时出发,绕着正方形的边按顺时针方向运动,当
同时出发,绕着正方形的边按顺时针方向运动,当![]() 点回到
点回到![]() 点时两点同时停止运动,运动时间为
点时两点同时停止运动,运动时间为![]() 秒.连接
秒.连接![]() ,线段
,线段![]() 、
、![]() 与正方形的边围成的面积较小部分的图形记为
与正方形的边围成的面积较小部分的图形记为![]() .
.
(1)请写出![]() 点的坐标.
点的坐标.
(2)若![]() 的速度均为1个单位长度秒,试判断在运动过程中,
的速度均为1个单位长度秒,试判断在运动过程中,![]() 的面积是否发生变化,如果不变求出该值,如果变化说明理由.
的面积是否发生变化,如果不变求出该值,如果变化说明理由.
(3)若![]() 点速度为2个单位长度秒,
点速度为2个单位长度秒,![]() 点为1个单位长度/秒,当
点为1个单位长度/秒,当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com