
【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
【答案】(1)y=﹣0.1x2+0.6x+1;
(2)年利润W(万元)与广告费用x(万元)的函数关系式为W=﹣x2+5x+10,每年投入的广告费是2.5万元时所获得的利润最大为16.25万元;(3)1≤x≤4时,年利润W(万元)不低于14万元.
【解析】试题分析:(1)二次函数的解析式为![]() 利用表格数据,即可求出
利用表格数据,即可求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)根据利润看作是销售总额减去成本费和广告费,利用配方法,结合![]() 的取值范围,可求最值.
的取值范围,可求最值.
![]() 令
令![]() ,求得
,求得![]() 的值,即可确定范围.
的值,即可确定范围.
试题解析:(1)设![]() 与
与![]() 的函数关系式为
的函数关系式为![]() 由题意,得
由题意,得
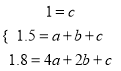 ,解得:
,解得: 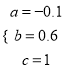 ,
,
∴函数的解析式为![]()
(2)根据题意,得![]()
![]()
![]()
∴当![]() 时,W最大=16.25.
时,W最大=16.25.
答:年利润W(万元)与广告费用![]() (万元)的函数关系式为
(万元)的函数关系式为![]() 每年投入的广告费是2.5万元时所获得的利润最大为16.25万元.
每年投入的广告费是2.5万元时所获得的利润最大为16.25万元.
(3)当![]() 时,
时,
![]()
解得: ![]()
![]() 时,年利润
时,年利润![]() (万元)不低于14万元.
(万元)不低于14万元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=![]() S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
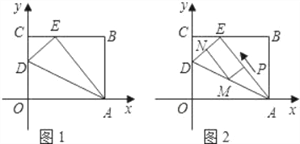
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
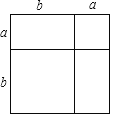
【题目】如图所示的大正方形是由两个小正方形和两个长方形组成.
(1)通过两种不同的方法计算大正方形的面积,可以得到一个数学等式;
(2)利用(1)中得到的结论,解决下面的问题:若a+b=2,ab=﹣3,
求:①a2+b2;
②a4+b4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.
(1)线段AC的长=________;
(2)当△PCF与△EDF相似时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
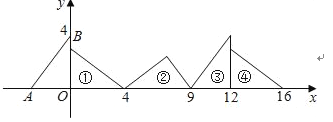
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
![]()
A. (60,0) B. (72,0) C. (67![]() ,
,![]() ) D. (79
) D. (79![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com