
【题目】背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五.它被记载于我国古代著名数学著作《周髀算经》中,在本题中,我们把三边的比为3∶4∶5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
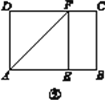
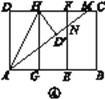
实践操作 如图①,在矩形纸片ABCD中,AD=8 cm,AB=12 cm.
第一步:如图②,将图①中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图④,将图③中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图②中证明四边形AEFD是正方形;
(2)请在图④中判断NF与ND′的数量关系,并加以证明;
(3)请在图④中证明△AEN是(3,4,5)型三角形.


【答案】(1)证明见解析(2)NF=ND′(3)证明见解析
【解析】
(1)根据矩形的性质得到∠D=∠DAE=90°,由折叠的性质得得到AE=AD,∠AEF=∠D=90°,求得∠D=∠DAE=∠AEF=90°,得到四边形AEFD是矩形,由于AE=AD,于是得到结论;
(2)连接HN,由折叠的性质得到∠AD′H=∠D=90°,HF=HD=HD′,根据正方形的想知道的∠HD′N=90°,根据全等三角形的性质即可得到结论;
(3)根据正方形的性质得到AE=EF=AD=8cm,由折叠得,AD′=AD=8cm,设NF=xcm,则ND′=xcm,根据勾股定理列方程得到x=2,于是得到结论;
(1)证明:∵四边形ABCD是矩形,
∴∠D=∠DAE=90°.
由折叠的性质得AE=AD,∠AEF=∠D=90°,∴∠D=∠DAE=∠AEF=90°,
∴四边形AEFD是矩形.
又∵AE=AD,∴矩形AEFD是正方形.
(2)NF=ND′.
证明:连接HN,由折叠的性质得∠AD′H=∠D=90°,HF=HD=HD′.
由(1)知四边形AEFD是正方形,∴∠EFD=90°.
∵∠AD′H=90°,∴∠HD′N=90°.
在Rt△HNF和Rt△HND′中,
∵HN=HN,HF=HD′,
∴Rt△HNF≌Rt△HND′,
∴NF=ND′.
(3)证明:由(1)知四边形AEFD是正方形,
∴AE=EF=AD=8 cm,
由折叠的性质得AD′=AD=8 cm.
设NF=x cm,则ND′=x cm.
在Rt△AEN中,∵AN2=AE2+EN2,∴(8+x)2=82+(8-x)2,解得x=2,∴AN=8+x=10 cm,EN=6 cm,∴EN∶AE∶AN=3∶4∶5,∴△AEN是(3,4,5)型三角形.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
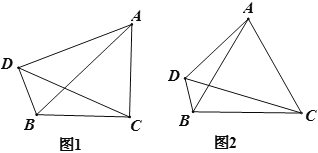
【题目】已知:在△ABC中,AC=BC,点D在△ABC外部,且∠ACB+∠ADB=180°,连接AB、CD.
(1)如图1,当∠ACB=90°时,则∠ADC=______°.
(2)如图2,当∠ACB=60°时,求证:DC平分∠ADB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种铂金饰品在甲、乙两种商店销售,甲店标价每克468元,按标价出售,不优惠,乙店标价每克525元,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.若购买的铂金饰品重量为![]() 克,其中
克,其中![]() .
.
(1)分别列出到甲、乙商店购买该种铂金饰品所需费用(用含x的代数式表示);
(2)李阿姨要买一条重量10克的此种铂金饰品,到哪个商店购买最合算;
(3)要买一条重量多少克的此种铂金饰品,才能到乙商店购买比到甲商店优惠300元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=60°,∠C=40°,DE垂直平分BC,连接BD.
(1)尺规作图:过点D作AB的垂线,垂足为F.(保留作图痕迹,不写作法)
(2)求证:点D到BA,BC的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
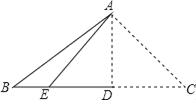
【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( )
A. 4 B. 6 C. 10 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部销售一种名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价
元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价![]() 元时,平均每天可多卖出
元时,平均每天可多卖出![]() 件.
件.
(1)若商场要求该服装部每天盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com