
【题目】某种铂金饰品在甲、乙两种商店销售,甲店标价每克468元,按标价出售,不优惠,乙店标价每克525元,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.若购买的铂金饰品重量为![]() 克,其中
克,其中![]() .
.
(1)分别列出到甲、乙商店购买该种铂金饰品所需费用(用含x的代数式表示);
(2)李阿姨要买一条重量10克的此种铂金饰品,到哪个商店购买最合算;
(3)要买一条重量多少克的此种铂金饰品,才能到乙商店购买比到甲商店优惠300元.
【答案】(1)甲商店:468x元;乙商店:(420x+315)元;(2)到乙商店购买最合算;(3)12.8125克.
【解析】
(1)根据两个商店的销售方法分别列式整理即可;
(2)把x=10分别代入(1)中列出的两个式子进行计算,然后比较即可得出结果;
(3)根据到乙商店购买比到甲商店优惠300元列方程求解即可.
解:(1)甲商店:468x;
乙商店:525×3+(x-3)×525×0.8=420x+315;
答:甲商店购买该种铂金饰品的费用为468x元;乙商店购买该种铂金饰品的费用为(420x+315)元;
(2)当x=10时,甲商店:468×10=4680(元),
乙商店:420×10+315=4515(元),
∵4680>4515,
答:到乙商店购买最合算;
(3)由题意得,468x-300=420x+315,
解得x=12.8125.
答:要买一条重量12.8125克的此种铂金饰品,才能到乙商店购买比到甲商店优惠300元.


科目:初中数学 来源: 题型:
【题目】如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.
(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.
(2)引申:如果∠C![]() 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____°时,图中阴影部分的面积和有最大值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥CD于点O,∠EOB=115°,求∠AOC的度数.请补全下面的解题过程(括号中填写推理的依据).
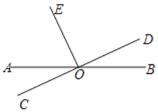
解:∵OE⊥CD于点O(已知),
∴______(______).
∵∠EOB=115°(已知),
∴∠DOB=______=115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC=______=25°(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,点D为BC的中点,BD=![]() AB,AD⊥BC.
AB,AD⊥BC.
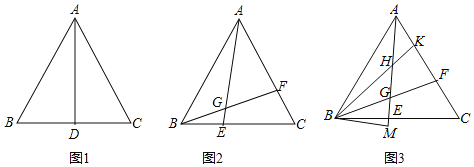
(1)如图1,求∠BAD的度数;
(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;
(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK=HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
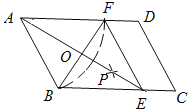
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五.它被记载于我国古代著名数学著作《周髀算经》中,在本题中,我们把三边的比为3∶4∶5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图①,在矩形纸片ABCD中,AD=8 cm,AB=12 cm.
第一步:如图②,将图①中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
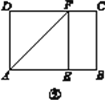
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
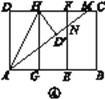
第三步:如图④,将图③中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图②中证明四边形AEFD是正方形;
(2)请在图④中判断NF与ND′的数量关系,并加以证明;
(3)请在图④中证明△AEN是(3,4,5)型三角形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知AD平分∠BAC,∠B+∠C=180°

(1)如图①,当∠B=90°时,求证:DB=DC;
(2)如图②,如果∠ABD<90°时,(1)中的结论还成立吗?如果成立,请给出证明,如果不成立,请举反例说明;
(3)如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=1,则ABAC=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个) | 售价(元/个) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com