
【题目】如图:已知AD平分∠BAC,∠B+∠C=180°

(1)如图①,当∠B=90°时,求证:DB=DC;
(2)如图②,如果∠ABD<90°时,(1)中的结论还成立吗?如果成立,请给出证明,如果不成立,请举反例说明;
(3)如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=1,则ABAC=___.
【答案】(1)见解析;(2)成立,理由见解析;(3)![]()
【解析】
(1)利用HL判断出△ADC≌△ADC,即可得出结论;
(2)先构造出△ACD≌△AED,得出DC=DE,∠AED=∠C,在判断出DE=DB,即可得出结论;
(3)利用(2)结论得出DE=DB,再判断出∠BDE=90°,利用勾股定理求出BE即可得出结论.
(1)∵∠B+∠C=180°,∠B=90°,
∴∠C=90°.
∵AD平分∠BAC,
∴∠DAC=∠BAD,
∵AD=AD,
∴△ACD≌△ABD(AAS),
∴BD=CD;
(2)BD=CD仍成立,
理由如下:如图②,在AB边上取点E,使AC=AE,

∵AD平分∠BAC,
∴∠CAD=∠EAD.
∵AD=AD,AC=AE,
∴△ACD≌△AED,
∴DC=DE,∠AED=∠C.
∵∠C+∠B=180°,∠AED+∠DEB=180°,
∴∠DEB=∠B,
∴DE=DB,
∴DB=DC;
(3)如图③,在AB上取一点E使AE=AC,
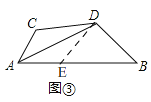
同(2)的方法得,AE=AC,CD=DE=BD=1,
∴∠DEB=∠B=45°,
∴∠BDE=90°,
根据勾股定理得,BE=![]() ,
,
∴AB-AC=BE=![]() ,
,
故答案为:![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
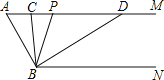
(1)求∠CBD的度数;
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种铂金饰品在甲、乙两种商店销售,甲店标价每克468元,按标价出售,不优惠,乙店标价每克525元,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.若购买的铂金饰品重量为![]() 克,其中
克,其中![]() .
.
(1)分别列出到甲、乙商店购买该种铂金饰品所需费用(用含x的代数式表示);
(2)李阿姨要买一条重量10克的此种铂金饰品,到哪个商店购买最合算;
(3)要买一条重量多少克的此种铂金饰品,才能到乙商店购买比到甲商店优惠300元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( )
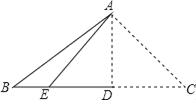
A. 4 B. 6 C. 10 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
根据你的观察,探究下面的问题:
(1)己知![]() ,求
,求![]() 的值.
的值.
(2)已知△ABC的三边长a、b、c都是正整数,且满足![]() ,求边c的最大值.
,求边c的最大值.
(3) 若己知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com