
����Ŀ����ͼ1�����ֱ��ԡ�ABC��AC��BC����Ϊ������������ı���ACDE��BCFGΪ�����Σ����������������Ϊ��չ˫Ҷ�����Σ�
��1�����֣���ͼ2������C=90��ʱ����֤����ABC���DCF�������ȣ�
��2�����꣺�����C![]() 90��ʱ����1���н��ۻ�������������������ͼ1����֤����������������˵�����ɣ�
90��ʱ����1���н��ۻ�������������������ͼ1����֤����������������˵�����ɣ�
��3�����ã���ͼ3���ֱ��ԡ�ABC������Ϊ������������ı���ACDE��BCFG��ABMNΪ�����Σ����������������Ϊ��չ��Ҷ�����Σ���֪��ABC�У�AC=3��BC=4������C=_____��ʱ��ͼ����Ӱ���ֵ�����������ֵ��________��

���𰸡���1��֤������������2��������֤������������3��18.
��������
���⣨1����ΪAC=DC����ACB=��DCF=90����BC=FC��������ABC�ա�DFC���Ӷ���ABC����DFC�������ȣ�
��2���ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q���õ��ı���ACDE��BCFG��Ϊ�����Σ�AC=CD��BC=CF����ACP=��DCQ��������APC�ա�DQC��
����AP=DQ������ΪS��ABC=![]() BCAP��S��DFC=
BCAP��S��DFC=![]() FCDQ������S��ABC=S��DFC��
FCDQ������S��ABC=S��DFC��
��3�����ݣ�2����ͼ����Ӱ���ֵ����������ABC�������������ͼ����Ӱ���ֵ�����������ֵ����������ABC����������ABC��ֱ�������Σ�����C��90��ʱ����Ӱ���ֵ�������������S��Ӱ���������=3S��ABC=3��![]() ��3��4=18��
��3��4=18��
��1��֤��������ABC����DFC�У�
��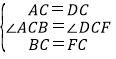 ��
��
���ABC�ա�DFC��
���ABC����DFC�������ȣ�
��2���⣺�������������£�
��ͼ���ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q��
���APC=��DQC=90����
���ı���ACDE��BCFG��Ϊ�����Σ�
��AC=CD��BC=CF����ACP+��PCD=90������DCQ+��PCD=90����
���ACP=��DCQ��
��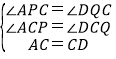 ��
��
��APC�ա�DQC��AAS����
��AP=DQ��
����S��ABC=![]() BCAP��S��DFC=
BCAP��S��DFC=![]() FCDQ��
FCDQ��
��S��ABC=S��DFC��
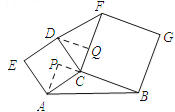
��3���⣺���ݣ�2����ͼ����Ӱ���ֵ����������ABC�����������
��ͼ����Ӱ���ֵ�����������ֵ����������ABC��������
������ABC��ֱ�������Σ�����C��90��ʱ����Ӱ���ֵ���������
��S��Ӱ���������=3S��ABC=3��![]() ��3��4=18��
��3��4=18��


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���мס������Ҵ�����ͬʱ��A��˳�����£��Ҵ���B�ؽӵ�֪ͨ���������������ϵ�����A��B������ͬһֱ�ߵ�C��ִ�����״�����˳������.��֪�ס��������ھ�ˮ�е��ٶȶ���ÿСʱ7.5ǧ�ף�ˮ�����ٶ�ΪÿСʱ2.5ǧ�ף�A��C���ؼ�ľ���Ϊ10ǧ��.����Ҵ���A�ؾ�B���ٵ���C�ع�����4Сʱ���ʣ��Ҵ���B�ص���C��ʱ���״�����B�ض�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ٻ����л��������ƺŵ�![]() ����ȹ����������Ⱥ����ޣ�����֭55%���ϣ����ܹ�����Ի�����ϲ��������20��
����ȹ����������Ⱥ����ޣ�����֭55%���ϣ����ܹ�����Ի�����ϲ��������20��![]() ����ȣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ,��¼���£�
����ȣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ,��¼���£�
��������IJ�ֵ ����λ��ǧ�ˣ� | -3 | -2 | -1��5 | 0 | 1 | 2��5 |
���� | 1 | 4 | 2 | 3 | 2 | 8 |
��1������20��![]() �������,���ص�һ��������һ���ض���ǧ�ˣ�
�������,���ص�һ��������һ���ض���ǧ�ˣ�
��2����������Ƚϣ�20��![]() ������ܼƳ����������ǧ�ˣ�
������ܼƳ����������ǧ�ˣ�
��3����![]() �����ÿǧ���ۼ�8Ԫ������20��
�����ÿǧ���ۼ�8Ԫ������20��![]() ����ȿ�������Ԫ��
����ȿ�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˷���ʽ��̽����Ӧ�ã�
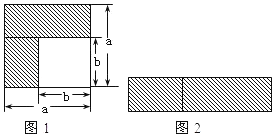
��1����ͼ1�����������Ӱ���ֵ������ ��д������ƽ�������ʽ����
��2����ͼ2��������Ӱ���ֲü�����������ƴ��һ�����Σ����Ŀ��� ������ ������� ��д�ɶ���ʽ�˷�����ʽ����
��3���Ƚ�ͼ1��ͼ2��Ӱ���ֵ���������Եõ���ʽ ��
��4�����������õ��Ĺ�ʽ���������и��⣺
��10.2��9.8���ڣ�2m+n��p����2m��n+p����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������һ���ڽ���ֱ�ǵ���������ֱ�������Σ�����ֱ�����ڵ������߽�ֱ�DZߣ�ֱ�����Եı߽�б�ߣ���ͼ����ʾ������ѧ�һ����֣���һ��ֱ���������У�����ֱ�DZ߳���ƽ���͵���б�߳���ƽ���������һ��ֱ�������ε�����ֱ�DZ߳��ȷֱ���![]() ��
��![]() ��б�߳�����
��б�߳�����![]() ����ô
����ô![]() ��
��
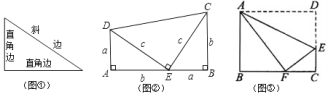
��1��ֱ���������ͼ�٣���a��3��b��4����c�� ����![]() ��
��![]() ����ֱ�������ε������ ______ ��
����ֱ�������ε������ ______ ��
��2���۲�ͼ�ڣ�����������ͬ��ֱ�������α�AE��EB��һ��ֱ���ϣ������ü���ͼ�ε�֮��������ϵ����˵��![]() ��
��
��3����ͼ����ʾ���۵�������ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪AB��8��BC��10����������Ľ�����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BΪԲ�ģ�BC��Ϊ�뾶�������ֱ�AC��AB��D��E������BD��DE������A=30����AB=AC�����BDE�Ķ���Ϊ�� ����

A.52.5��B.60��C.67.5��D.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�鳤�Ϳ��ֱ�Ϊ60����40���ij�������Ƥ��Ҫ�������Ľǽ�ȥ�ĸ���ȵ�С�����Σ��۳�һ���ǵij�����ˮ�ۣ�ʹ���ĵ����Ϊ800ƽ������.���ȥ�����εı߳�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AM��BN����A=60������P������AM��һ���㣨���A���غϣ���BC��BD�ֱ�ƽ�֡�ABP�͡�PBN���ֱ�����AM�ڵ�C��D��
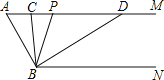
��1�����CBD�Ķ�����
��2������P�˶�ʱ����APB����ADB�ı�ֵ�Ƿ���֮�仯�������䣬����������ֵ�����仯�����ҳ��仯���ɣ�
��3������P�˶���ij��ʱ����ACB=��ABD�����ʱ��ABC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�����Ʒ�ڼס��������̵����ۣ�����ÿ��468Ԫ������۳��ۣ����Żݣ��ҵ���ÿ��525Ԫ��������IJ�����Ʒ��������3�ˣ������ֿɴ���۳��ۣ�������IJ�����Ʒ����Ϊ![]() �ˣ�����
�ˣ�����![]() ��
��
��1���ֱ��г����ס����̵깺����ֲ�����Ʒ������ã��ú�x�Ĵ���ʽ��ʾ����
��2�����Ҫ��һ������10�˵Ĵ��ֲ�����Ʒ�����ĸ��̵깺������㣻
��3��Ҫ��һ���������ٿ˵Ĵ��ֲ�����Ʒ�����ܵ����̵깺��ȵ����̵��Ż�300Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com