
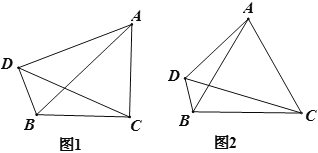
【题目】已知:在△ABC中,AC=BC,点D在△ABC外部,且∠ACB+∠ADB=180°,连接AB、CD.
(1)如图1,当∠ACB=90°时,则∠ADC=______°.
(2)如图2,当∠ACB=60°时,求证:DC平分∠ADB.
【答案】(1)45°;(2)证明见解析.
【解析】
(1)延长AD和CB,相交于点E,如图1,先判断△ABC为等腰直角三角形得到∠ABC=45°,再利用等角的余角可得∠BDE=∠ACB,则可判断△EBD∽△EAC,所以ED:EC=EB:EA,则ED:EB=EC:EA,加上∠DEC=∠BEA,则可判断△EDC∽△EBA,所以∠2=∠1,然后利用三角形内角和定理可得∠ADC=∠ABC=45°;
(2)延长AD和CB,相交于点E,如图2,先判断△ABC为等边三角形得到∠ABC=60°,与(1)一样可证明∠2=∠1,则∠ADC=∠ABC=60°,再计算出∠BDC=60°,于是可判断DC平分∠ADB.
(1)延长AD和CB,相交于点E,如图1,∵AC=BC,∠ACB=90°,
∴△ABC为等腰直角三角形,
∴∠ABC=45°,
∵∠ACB+∠ADB=180°,
而∠BDE+∠ADB=180°,∴∠BDE=∠ACB,
而∠BED=∠AEC,∴△EBD∽△EAC,
∴ED:EC=EB:EA,
∴ED:EB=EC:EA,
而∠DEC=∠BEA,∴△EDC∽△EBA,

∴∠2=∠1,
∴∠ADC=∠ABC=45°,
(2)证明:延长AD和CB,相交于点E,如图2,
∵AC=BC,∠ACB=60°,
∴△ABC为等边三角形,
∴∠ABC=60°,
与(1)一样可证明△EDC∽△EBA,
∴∠2=∠1,
∴∠ADC=∠ABC=60°,
而∠ADB=180°-∠ACB=60°=120°,
∴∠BDC=60°,
∴DC平分∠ADB.


科目:初中数学 来源: 题型:
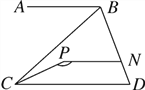
【题目】如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥CD于点O,∠EOB=115°,求∠AOC的度数.请补全下面的解题过程(括号中填写推理的依据).
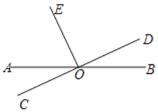
解:∵OE⊥CD于点O(已知),
∴______(______).
∵∠EOB=115°(已知),
∴∠DOB=______=115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC=______=25°(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,点D为BC的中点,BD=![]() AB,AD⊥BC.
AB,AD⊥BC.
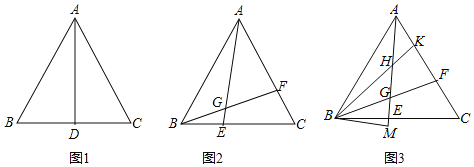
(1)如图1,求∠BAD的度数;
(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;
(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK=HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
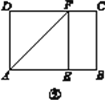
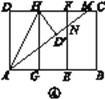
【题目】背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五.它被记载于我国古代著名数学著作《周髀算经》中,在本题中,我们把三边的比为3∶4∶5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图①,在矩形纸片ABCD中,AD=8 cm,AB=12 cm.
第一步:如图②,将图①中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图④,将图③中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图②中证明四边形AEFD是正方形;
(2)请在图④中判断NF与ND′的数量关系,并加以证明;
(3)请在图④中证明△AEN是(3,4,5)型三角形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将一副三角板(直角三角板![]() 和直角三角板
和直角三角板![]() )的两个顶点重合于点
)的两个顶点重合于点![]() .
.
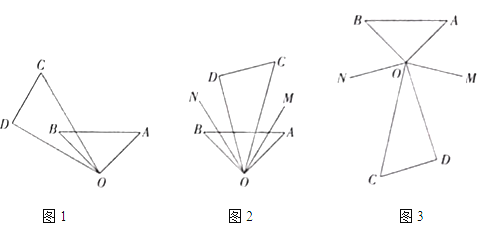
(1)如图1,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,当
逆时针方向转动,当![]() 恰好平分
恰好平分![]() 时,
时,![]() 的度数是 _.
的度数是 _.
(2)如图2,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,如果三角板
,如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
(3)当三角板![]() 绕点
绕点![]() 继续转动到如图3所示的位置时,作射线
继续转动到如图3所示的位置时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,请你求出此时钝角
,请你求出此时钝角![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com