
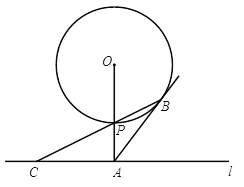
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见试题解析;(2)3.
【解析】试题分析:(1)由同圆半径相等和对顶角相等得∠OBP=∠APC,由圆的切线性质和垂直得∠ABP+∠OBP=90°和∠ACB+∠APC=90°,则∠ABP=∠ACB,根据等角对等边得AB=AC;
(2)设⊙O的半径为r,分别在Rt△AOB和Rt△ACP中根据勾股定理列等式,并根据AB=AC得52﹣r2=(2![]() )2﹣(5﹣r)2,求出r的值即可.
)2﹣(5﹣r)2,求出r的值即可.
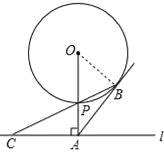
试题解析:(1)连接OB,∵OB=OP,∴∠OPB=∠OBP,∵∠OPB=∠APC,
∴∠OBP=∠APC,∵AB与⊙O相切于点B,∴OB⊥AB,∴∠ABO=90°,
∴∠ABP+∠OBP=90°,∵OA⊥AC,∴∠OAC=90°,∴∠ACB+∠APC=90°,∴∠ABP=∠ACB,
∴AB=AC;
(2)设⊙O的半径为r,在Rt△AOB中,AB2=OA2﹣OB2=52﹣r2,
在Rt△ACP中,AC2=PC2﹣PA2,AC2=(2![]() )2﹣(5﹣r)2,
)2﹣(5﹣r)2,
∵AB=AC,∴52﹣r2=(2![]() )2﹣(5﹣r)2,解得:r=3,
)2﹣(5﹣r)2,解得:r=3,
则⊙O的半径为3.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
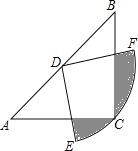
A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系xOy中,△ABC三点的坐标分别为A(-1,0),B(-4,4),C(0,3).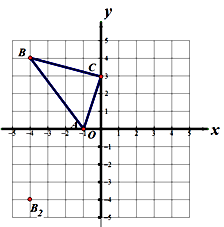
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;写出B1的坐标为.
(2)填空:在图中,若B2(-4,-4)与点B关于一条直线成轴对称,则这条对称轴是 , 此时点C关于这条直线的对称点C2的坐标为;
(3)在y轴上确定一点P,使△APB的周长最小.(注:简要说明作法,保留作图痕迹,不求坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
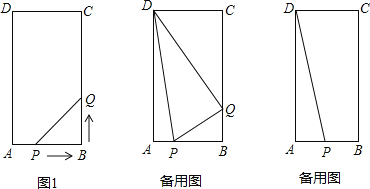
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确的命题个数有( )
(1)已知⊙O的半径为1,AB是⊙O的一条弦,AB=![]() ,则弦AB所对圆周角的度数为60度;
,则弦AB所对圆周角的度数为60度;
(2)已知⊙O的半径为5,圆心O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有3个;
(3)平分弦的直径垂直于弦;
(4)已知点P是线段AB的黄金分割点,若AB=1,AP=![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】-6xn-3x2n分解因式正确的是( )
A. 3(-2xn-x2n) B. -3xn(2+xn) C. -3(2xn+x2n) D. -3xn(xn+2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com