
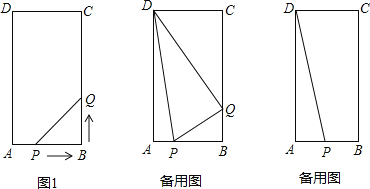
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
【答案】(1)t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2;
(2)△DPQ为直角三角形;
(3)运动开始后第6![]() ﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.
﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.
【解析】试题分析:(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;(2)表示出DP2=![]() ,PQ2=
,PQ2=![]() ,DQ2=117,进而得到PQ2+DQ2=DP2,得出答案;(3)假设运动开始后第x秒时,满足条件,则有QP=QD,表示出QP2,QD2,列出等式,整理得到方程,求出方程的解,根据时间大于0秒小于6秒,即可解答.
,DQ2=117,进而得到PQ2+DQ2=DP2,得出答案;(3)假设运动开始后第x秒时,满足条件,则有QP=QD,表示出QP2,QD2,列出等式,整理得到方程,求出方程的解,根据时间大于0秒小于6秒,即可解答.
试题解析:(1)设经过t秒,△PBQ的面积等于8cm2,
则:BP=6﹣t,BQ=2t,
所以![]() ×(6﹣t)×2t=8,即t2﹣6t+8=0,
×(6﹣t)×2t=8,即t2﹣6t+8=0,
可得:t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2.
(2)当t=![]() 秒时,
秒时,
AP=![]() ,BP=6﹣
,BP=6﹣![]() =
=![]() ,BQ=
,BQ=![]() ×2=3,CQ=12﹣3=9,
×2=3,CQ=12﹣3=9,
∴在Rt△DAP中,![]() ,
,
在Rt△DCQ中,DQ2=DC2+CQ2=62+92=117,
在Rt△QBP中,![]() ,
,
∴![]() ,
,
∴DQ2+QP2=DP2,
∴△DPQ为直角三角形;
(3)假设运动开始后第x秒时,满足条件,则:QP=QD,
∵OP2=PB2+BQ2=(6﹣x)2+(2x)2,
QD2=QC2+CD2=(12﹣2x)2+62,
∴(12﹣2x)2+62=(6﹣x)2+(2x)2,
整理,得:x2+36x﹣144=0,
解得:x=﹣18±6![]() ,
,
∵0<6![]() ﹣18<6,
﹣18<6,
∴运动开始后第6![]() ﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.
﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的平分分别为:90,85,90,80,95,则这组数据的众数是( )
A.95
B.90
C.85
D.80
查看答案和解析>>
科目:初中数学 来源: 题型:
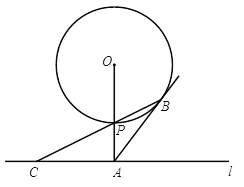
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com