
【题目】综合题
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
【答案】
(1)解:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°﹣∠DCB =∠BCE.
在△ACD和△BCE中,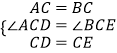 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°
(2)解:∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°
∴CA=CB,CD=CE.
且∠ACD=∠BCE.
在△ACD和△BCE中,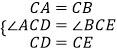 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM
【解析】(1) 抓住已知条件△ACB和△DCE均为等边三角形,得出CA=CB,CD=CE,∠ACB=∠DCE=60°,观察图形证明∠ACD =∠BCE,再利用SAS证明△ACD≌△BCE,得出∠ADC=∠BEC,然后求出∠ADC的度数,就可得出∠BEC的度数,利用∠AEB=∠BEC﹣∠CED,得出结果即可。
(2)根据已知易证△ACD≌△BCE,根据全等三角形的性质证出AD=BE,∠ADC=∠BEC.再求出∠ADC、∠BEC的度数,去证明∠AEB是直角,然后证明DM=ME=CM,就可证得线段CM,AE,BE之间的数量关系。


科目:初中数学 来源: 题型:
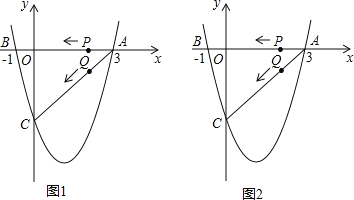
【题目】如图1(注:与图2完全相同),二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积;
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
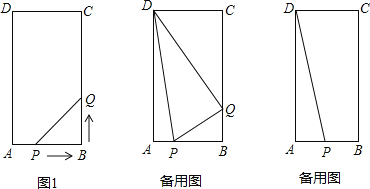
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确的命题个数有( )
(1)已知⊙O的半径为1,AB是⊙O的一条弦,AB=![]() ,则弦AB所对圆周角的度数为60度;
,则弦AB所对圆周角的度数为60度;
(2)已知⊙O的半径为5,圆心O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有3个;
(3)平分弦的直径垂直于弦;
(4)已知点P是线段AB的黄金分割点,若AB=1,AP=![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一生产季节性产品的企业,有两种营销方案,经测算:方案一,一年中获得的每月利润y(万元)和月份x的关系为![]() ;方案二,一年中获得的每月利润y(万元)与月份x的关系为
;方案二,一年中获得的每月利润y(万元)与月份x的关系为![]() .两个函数部分图象如图所示:
.两个函数部分图象如图所示:

(1)请你指出:方案一,月利润对应的图象是 ;方案二,月利润对应的图象是 ;(填序号)
(2)该企业一年中月利润最高可达 万元;
(3)生产季节性产品的企业,当它的产品无利润时就会立即停 产,企业原计划全年使用营销方案二进行销售,
则①该企业一年中应停产的月份是 ;
②为了使全年能获得更高利润,企业应该如何改进其营销方案,使全年总利润最高?并算出全年最高总利润比原计划多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4: 3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
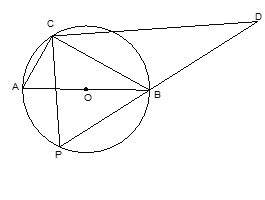
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com