
【题目】现有一生产季节性产品的企业,有两种营销方案,经测算:方案一,一年中获得的每月利润y(万元)和月份x的关系为![]() ;方案二,一年中获得的每月利润y(万元)与月份x的关系为
;方案二,一年中获得的每月利润y(万元)与月份x的关系为![]() .两个函数部分图象如图所示:
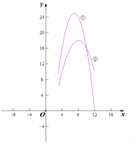
.两个函数部分图象如图所示:

(1)请你指出:方案一,月利润对应的图象是 ;方案二,月利润对应的图象是 ;(填序号)
(2)该企业一年中月利润最高可达 万元;
(3)生产季节性产品的企业,当它的产品无利润时就会立即停 产,企业原计划全年使用营销方案二进行销售,
则①该企业一年中应停产的月份是 ;
②为了使全年能获得更高利润,企业应该如何改进其营销方案,使全年总利润最高?并算出全年最高总利润比原计划多多少?
【答案】(1) ②, ①;(2)25;(3) ①1月,2月 ,12月; ②从2月份到10月份选择方案二,11月份和12月份选择方案一,可以使全年总利润最高;去年最高总利润比原计划多23.5万元.
【解析】试题分析: (1)将方案一和方案二的解析式化为顶点式,即可得到相应的最大值,再结合函数图象即可解答本题;
(2)将方案一和方案二的解析式化为顶点式,即可得到相应的最大值,本题得以解决;
(3)①解答本题只要算出方案一和方案二都等于0的情况,即可得到哪个月份需要停产;
②解答本题只要算出方案一不小于方案二的情况,即可得到最优方案,从而可以得到去年最高总利润比原计划多多少.
试题解析:
(1)方案一:y=0.5x2+8x14=0.5(x216x)14=0.5(x8)2+18,y的最大值是18,
方案二:y=x2+14x24=(x7)2+25,y的最大值是25,
∴方案一月利润对应的函数图象是②,方案二对应的图象是①,
故答案为:②,①;
(2)∵方案一:y=0.5x2+8x14=0.5(x216x)14=0.5(x8)2+18,y的最大值是18,
方案二:y=x2+14x24=(x7)2+25,y的最大值是25,
∴该企业一年中月利润最高可达25万元,
故答案为:25;
(3)①将y=0代入y=0.5x2+8x14,得x=2或x=14,故方案一停产的月份是1月份、2月份;
将y=0代入y=x2+14x24,得x=2或x=12,故方案二停产的月份是1月份、2月份、12月份;
故答案为:方案一是1月份和2月份,方案二是1月份、2月份、12月份;
②令﹣0.5x2+8x﹣14=﹣x2+14x﹣24,得x=2或x=10,
∴从2月份到10月份选择方案二,11月份和12月份选择方案一,可以使全年总利润最高;
∴去年最高总利润比原计划多的钱数是:
(-0.5×112+8×11﹣14)+(﹣0.5×122+8×12﹣14)=23.5(万元),
即去年最高总利润比原计划多23.5万元.


科目:初中数学 来源: 题型:
【题目】某文化用品商店在开学初用2000元购进一批学生书包,按每个120元出售,很快销售一空,于是商店又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元,仍按120元出售,最后剩下4个按八折卖出,这笔生意该店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由.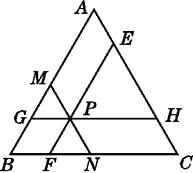
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若xa+2+yb﹣1+3=0是关于x,y的二元一次方程,则a、b的值为( )
A.a=﹣1,b=2
B.a=﹣1,b=1
C.a=1,b=1
D.a=1,b=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断:![]()
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com