Question

【题目】如图，圆O的直径为5，在圆O上位于直径AB的异侧有定点C和动点P，已知BC：CA=4： 3，点P在半圆弧AB上运动（不与A、B两点重合），过点C作CP的垂线CD交PB的延长线于D点．

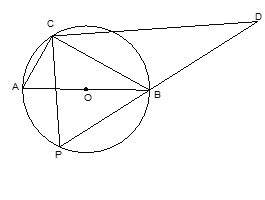
（1）求证：AC·CD=PC·BC；

（2）当点P运动到AB弧中点时，求CD的长；

（3）当点P运动到什么位置时，△PCD的面积最大？并求出这个最大面积S。

Answer 1

【答案】（1）见解析（2）（3）

【解析】（1）由题意，AB是⊙O的直径；∴∠ACB=90。，∵CD⊥CP，∴∠PCD=90。

∴∠ACP+∠BCD=∠PCB+∠DCB=90。，∴∠ACP=∠DCB，又∵∠CBP=∠D+∠DCB，∠CBP=∠ABP+∠ABC，∴∠ABC=∠APC，∴∠APC＝∠D，∴△PCA∽△DCB；∴，∴AC·CD=PC·BC

（2）当P运动到AB弧的中点时,连接AP，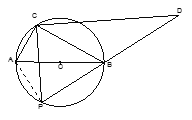

∵AB是⊙O的直径，∴∠APB=90。，又∵P是弧AB的中点，∴弧PA=弧PB，∴AP=BP，∴∠PAB=∠PBA=45.,又AB=5，∴PA=，过A作AM⊥CP，垂足为M，在Rt△AMC中，∠ACM=45，∴∠CAM=45，∴AM=CM=，在Rt△AMP中，AM2+AP2=PM2，∴PM=，∴PC=PM+=。由（1）知：AC·CD=PC·BC ，3×CD=PC×4，∴CD＝

（3）由（1）知：AC·CD=PC·BC，所以AC：BC=CP：CD；

所以CP：CD=3：4，而△PCD的面积等于·=，

CP是圆O的弦，当CP最长时，△PCD的面积最大，而此时C

P就是圆O的直径；所以CP=5，∴3：4=5：CD；

∴CD=，△PCD的面积等于·==；

（1）通过求证△PCA∽△DCB，即可求证AC·CD=PC·BC

（2）当P运动到AB弧的中点时,连接AP，求出PA，过A作AM⊥CP，垂足为M，求出AM，

从而求出PC ,由（1）可知CD的长

（3）当CP最长时，即为圆的直径，△PCD的面积最大，由（1）可求得CD的长，从而求出△PCD的面积