
【题目】如图5, ![]() A=80
A=80 ![]() ,点O是AB,AC垂直平分线的交点,则
,点O是AB,AC垂直平分线的交点,则 ![]() BC0的度数是( )
BC0的度数是( )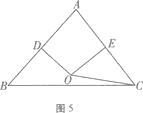
A.40 ![]()
B.30 ![]()
C.20 ![]()
D.10 ![]()
【答案】D
【解析】解 : 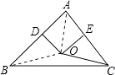
连接OA、OB,
∵∠A=80 ,
∴∠ABC+∠ACB=100 ,
∵O是AB,AC垂直平分线的交点,
∴OA=OB,OA=OC,
∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=80 ,
∴∠OBC+∠OCB=10080=20 ,
∵OB=OC,
∴∠BCO=∠CBO=10,
故应选 :D。
连接OA、OB,根据三角形内角和定理求出∠ABC+∠ACB=100°,根据线段的垂直平分线的性质得到OA=OB,OA=OC,根据等边对等角及等量代换得出∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,根据等来那个代换及角的和差得出∠OBC+∠OCB=10080=20 , 根据等腰三角形的性质计算即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
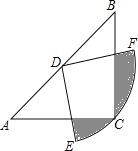
A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确的命题个数有( )
(1)已知⊙O的半径为1,AB是⊙O的一条弦,AB=![]() ,则弦AB所对圆周角的度数为60度;
,则弦AB所对圆周角的度数为60度;
(2)已知⊙O的半径为5,圆心O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有3个;
(3)平分弦的直径垂直于弦;
(4)已知点P是线段AB的黄金分割点,若AB=1,AP=![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4: 3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
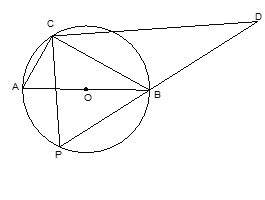
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】-6xn-3x2n分解因式正确的是( )
A. 3(-2xn-x2n) B. -3xn(2+xn) C. -3(2xn+x2n) D. -3xn(xn+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解本校九年级男生体育测试项目“立定跳远”的训练情况,体育老师随机抽査了该年级若干名男生,对他们进行了严格的测试,同时统计了每个人的成绩(成绩记为![]() 米).现将结果分为四个等级:优秀(
米).现将结果分为四个等级:优秀(![]() ),良好(
),良好(![]() )、及格(
)、及格(![]() )和不及格(
)和不及格(![]() ).并将统计结果绘制成如下两副不完整的统计图.
).并将统计结果绘制成如下两副不完整的统计图.
请你根据以上信息,解答下列问题:
(![]() )补全条形统计图和扇形统计图.
)补全条形统计图和扇形统计图.
(![]() )被测试男生成绩等级的中位数落在________等级.
)被测试男生成绩等级的中位数落在________等级.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com