
【题目】如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
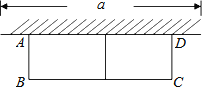
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大,最大面积为多少m2?
【答案】(1)S=﹣3x2+24x,![]() ;(2)AB长为5m;(3)当AB的长是
;(2)AB长为5m;(3)当AB的长是![]() 米时,围成的花圃的面积最大,最大面积为
米时,围成的花圃的面积最大,最大面积为![]() m2.
m2.
【解析】
(1)根据篱笆的长度为24m,AB=xm,即可得出BC=(24-3x)m,根据矩形的面积公式即可写出函数关系式,再利a的最大长度为10m,即可得出x的取值范围.
(2)根据题(1)得出的函数关系式,令面积为45即可得出结果,将得出的x的值带入验算,得出满足题意的值.
(3)根据配方法将函数解析式配成顶点式,结合自变量的取值范围即可得出最大面积.
解:(1)根据题意,得S=x(24﹣3x),
即所求的函数解析式为:S=﹣3x2+24x,
又∵0<24﹣3x≤10,
∴![]() ,
,
(2)根据题意,设AB长为x,则BC长为24﹣3x
∴﹣3x2+24x=45.
整理,得x2﹣8x+15=0,
解得x=3或5,
当x=3时,BC=24﹣9=15>10不成立,
当x=5时,BC=24﹣15=9<10成立,
∴AB长为5m;
(3)S=24x﹣3x2=﹣3(x﹣4)2+48
∵墙的最大可用长度为10m,0≤BC=24﹣3x≤10,
∴![]() ,
,
∵对称轴x=4,开口向下,
∴当x=![]() m,有最大面积的花圃.
m,有最大面积的花圃.
即:x=![]() m,
m,
最大面积为:24×![]() ﹣3×(
﹣3×(![]() )2=
)2=![]() m2
m2


科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的周长为12,E,F,G,H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(1)请直接写出y与x之间的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
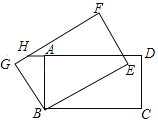
【题目】如图,在矩形ABCD中,AB=4,BC=6,将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF,延长DA交FG于点H,则GH的长为( )
A.8﹣4![]() B.
B.![]() ﹣4C.3
﹣4C.3![]() ﹣4D.6﹣3
﹣4D.6﹣3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
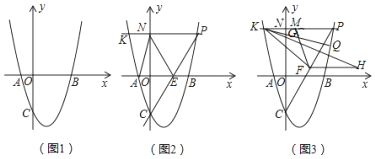
(1)如图1,求抛物线的解析式;
(2)如图2,点P是第一象限抛物线上的一个动点,连接CP交x轴于点E,过点P作PK∥x轴交抛物线于点K,交y轴于点N,连接AN、EN、AC,设点P的横坐标为t,四边形ACEN的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点F是PC中点,过点K作PC的垂线与过点F平行于x轴的直线交于点H,KH=CP,点Q为第一象限内直线KP下方抛物线上一点,连接KQ交y轴于点G,点M是KP上一点,连接MF、KF,若∠MFK=∠PKQ,MP=AE+![]() GN,求点Q坐标.
GN,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
 A、2
A、2
B、4
C、![]()
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
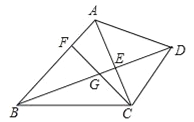
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
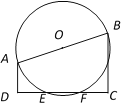
【题目】如图,梯形ABCD中,AD∥BC,∠ADC=90,AD= 2,BC= 4,![]() .以AB为直径作⊙O,交边DC于E、F两点.
.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF.
(2)求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=![]() ∠DOQ.
∠DOQ.
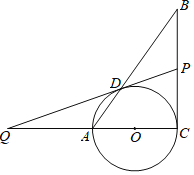
(1)求证:PD是⊙O的切线;
(2)若AQ=AC,AD=4时,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com