
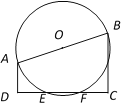
【题目】如图,梯形ABCD中,AD∥BC,∠ADC=90,AD= 2,BC= 4,![]() .以AB为直径作⊙O,交边DC于E、F两点.
.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF.
(2)求直径AB的长.
【答案】(1)证明见解析;(2)AB=![]() .
.
【解析】
(1)首先根据AD∥BC,∠ADC=90,OH⊥DC,得出AD∥OH∥BC,进而根据OA=OB得出DH=HC,然后根据垂径定理得出EH = HF,进而得出DE=CF;
(2)首先根据∠AGB =∠BCN = 90°,得出AG∥DC,然后根据AD∥BC,得出AD=CG.,进而得出BG,再根据三角函数得出AG,最后根据勾股定理得出AB.

(1)过点O作OH⊥DC,垂足为H.
∵AD∥BC,∠ADC=90,OH⊥DC,
∴∠BCN=∠OHC=∠ADC =90.
∴AD∥OH∥BC.
又∵OA=OB.
∴DH=HC.
∵OH⊥DC,OH过圆心,
∴EH = HF.
∴DH-EH =HC-HF.
即:DE=CF.
(2)过点A作AG⊥BC,垂足为点G,∠AGB = 90°,
∵∠AGB =∠BCN = 90°,
∴AG∥DC.
∵AD∥BC,
∴AD=CG.
∵AD= 2,BC= 4,
∴BG= BC-CG =2.
在Rt△AGB中,∵![]() ,
,
∴![]() .
.
在Rt△AGB中,![]()
∴AB=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意两点M![]() ,N
,N![]() ,给出如下定义:点M与点N的“折线距离”为:
,给出如下定义:点M与点N的“折线距离”为:![]()
![]()
![]() .
.

例如:若点M(-1,1),点N(2,-2),则点M与点N的“折线距离”为:![]() .根据以上定义,解决下列问题:
.根据以上定义,解决下列问题:
(1)已知点P(3,-2).
①若点A(-2,-1),则d(P,A)= ;
②若点B(b,2),且d(P,B)=5,则b= ;
③已知点C(m,n)是直线![]() 上的一个动点,且d(P,C)<3,求m的取值范围.
上的一个动点,且d(P,C)<3,求m的取值范围.
(2)⊙F的半径为1,圆心F的坐标为(0,t),若⊙F上存在点E,使d(E,O)=2,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
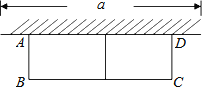
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大,最大面积为多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y=![]() (k≠0)经过点C,则k的值为( )
(k≠0)经过点C,则k的值为( )
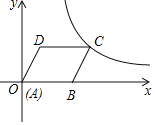
A.12B.15C.20D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③DP2=PHPC;④FE:BC=![]() ,其中正确的个数为( )
,其中正确的个数为( )
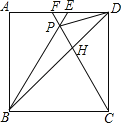
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字分别是1,2,3,4 的四张扑克牌背面朝上,洗匀后放在桌面上.

(1)从中随机抽出一张牌,牌面数字是偶数的概率是_____;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是 4 的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;
②b>2a;
③ax2+bx+c=0的两根分别为﹣3和1;
④c=﹣3a,
其中正确的命题是( )
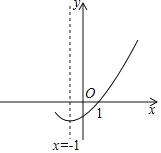
A.①②B.②③C.①③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解早高峰期间A,B两邻近地铁站乘客的乘车等待时间(指乘客从进站到乘上车的时间),某部门在同一上班高峰时段对A、B两地铁站各随机抽取了500名乘客,收集了其乘车等待时间(单位:分钟)的数据,统计如表:
等待时的频数间 乘车等待时间 地铁站 | 5≤t≤10 | 10<t≤15 | 15<t≤20 | 20<t≤25 | 25<t≤30 | 合计 |
A | 50 | 50 | 152 | 148 | 100 | 500 |
B | 45 | 215 | 167 | 43 | 30 | 500 |
据此估计,早高峰期间,在A地铁站“乘车等待时间不超过15分钟”的概率为_____;夏老师家正好位于A,B两地铁站之间,她希望每天上班的乘车等待时间不超过20分钟,则她应尽量选择从_____地铁站上车.(填“A”或“B”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com