
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=![]() ∠DOQ.
∠DOQ.
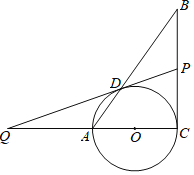
(1)求证:PD是⊙O的切线;
(2)若AQ=AC,AD=4时,求BP的长.
【答案】(1)详见解析;(2)2![]()
【解析】
(1)连结DC,根据圆周角定理得到∠DCA=![]() ∠DOA,由∠ADQ=
∠DOA,由∠ADQ=![]() ∠DOQ,可得∠DCA=∠ADQ,根据余角的性质得到∠ADQ+∠ADO=90°,即可得结论;
∠DOQ,可得∠DCA=∠ADQ,根据余角的性质得到∠ADQ+∠ADO=90°,即可得结论;
(2)根据切线的判定定理得到PC是⊙O切线,得PD=PC,连接OP,可证得OP∥AD,根据平行线分线段长比例定理得到OP的长,根据三角形中位线定理得AB的长,最后由射影定理即可求出结果.
解:(1)连接DC,
∵![]() ,
,
∴∠DCA=![]() ∠DOA,
∠DOA,
∵∠ADQ=![]() ∠DOQ,
∠DOQ,
∴∠DCA=∠ADQ,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DCA+∠DAC=90°,
∴∠ADQ+∠DAC=90°,
∵∠ADO=∠DAC,
∴∠ADQ+∠ADO=90°,
∴![]() ,即DP是⊙O切线;
,即DP是⊙O切线;
(2)∵∠C=90°,OC为半径.
∴PC是⊙O切线,
∴PD=PC,
连接OP,
∴∠DPO=∠CPO,
∴OP⊥CD,
∴OP∥AD,
∵AQ=AC=2OA,
∴![]() ,
,
∵AD=4,
∴OP=6,
∵O为AC中点、OP∥AD,则OP是△ACB的中位线,
∴AB=12,
∵CD⊥AB,∠ACB=90°,
∴BC2=BDBA=96,
∴BC=![]() ,
,
∴BP=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
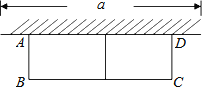
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大,最大面积为多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;
②b>2a;
③ax2+bx+c=0的两根分别为﹣3和1;
④c=﹣3a,
其中正确的命题是( )
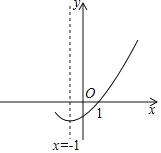
A.①②B.②③C.①③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.

(1)当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是 ;
②点T在直线y=﹣![]() x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣2x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,请求出圆心C的横坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是( )

①△BCD为等腰三角形;②BF=AC;③CE=![]() BF;④BH=CE.
BF;④BH=CE.
A. ①② B. ①③ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解早高峰期间A,B两邻近地铁站乘客的乘车等待时间(指乘客从进站到乘上车的时间),某部门在同一上班高峰时段对A、B两地铁站各随机抽取了500名乘客,收集了其乘车等待时间(单位:分钟)的数据,统计如表:
等待时的频数间 乘车等待时间 地铁站 | 5≤t≤10 | 10<t≤15 | 15<t≤20 | 20<t≤25 | 25<t≤30 | 合计 |
A | 50 | 50 | 152 | 148 | 100 | 500 |
B | 45 | 215 | 167 | 43 | 30 | 500 |
据此估计,早高峰期间,在A地铁站“乘车等待时间不超过15分钟”的概率为_____;夏老师家正好位于A,B两地铁站之间,她希望每天上班的乘车等待时间不超过20分钟,则她应尽量选择从_____地铁站上车.(填“A”或“B”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(0,﹣3).
(1)求点A、B的坐标;
(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;
(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com