
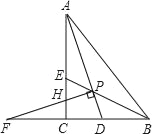
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】D
【解析】根据三角形内角和定理以及角平分线定义判断①;根据全等三角形的判定和性质判断②③;根据角平分线的判定与性质判断④.
在△ABC中,∵∠ACB=90°,
∴∠BAC+∠ABC=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=![]() (∠BAC+∠ABC)=45°,
(∠BAC+∠ABC)=45°,
∴∠APB=135°,故①正确.
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
又∵∠ABP=∠FBP,BP=BP,
∴△ABP≌△FBP,
∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.
在△APH和△FPD中,
∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠BFP,PA=PF,
∴△APH≌△FPD,
∴PH=PD,故③正确.
∵△ABC的角平分线AD、BE相交于点P,
∴点P到AB、AC的距离相等,点P到AB、BC的距离相等,
∴点P到BC、AC的距离相等,
∴点P在∠ACB的平分线上,
∴CP平分∠ACB,故④正确.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.

(1)请你猜想BH和AC的关系,并说明理由;
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
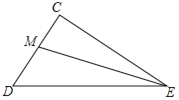
【题目】如图, ![]() ,EM平分
,EM平分![]() ,并与CD边交于点M.DN平分
,并与CD边交于点M.DN平分![]() ,
,
并与EM交于点N.
(1)依题意补全图形,并猜想![]() 的度数等于 ;
的度数等于 ;
(2)证明以上结论.
证明:∵ DN平分![]() ,EM平分
,EM平分![]() ,
,
∴![]() ,
,
![]() = .
= .
(理由: )
∵![]() ,
,
∴![]() = ×(∠ +∠ )= ×90°= °.
= ×(∠ +∠ )= ×90°= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017四川省凉山州,第24题,8分)为了推进我州校园篮球运动的发展,2017年四川省中小学生男子篮球赛于2月在西昌成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:

(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:![]() N:
N:![]() ,其中
,其中![]() ,以下列四个结论中,错误的是( )
,以下列四个结论中,错误的是( )
A、如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
B、如果方程M有两根符号相同,那么方程N的两根符号也相同;
C、如果5是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
D、如果方程M和方程N有一个相同的根,那么这个根必是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com