Question

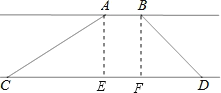
【题目】如图，两条互相平行的河岸，在河岸一边测得AB为20米，在另一边测得CD为70米，用测角器测得∠ACD=30°，测得∠BDC=45°，求两条河岸之间的距离．（， ≈1.7，结果保留整数）

Answer 1

【答案】两条河岸之间的距离约为18米．

【解析】试题分析：分别过点A、B作CD的垂线交CD于点E、F，令两条河岸之间的距离为h．则AE=BF=h，EF=AB=20．解Rt△ACE，得出CE=h，解Rt△BDF，求出DF=BF=h，根据CD=CE+EF+FD=70列出方程，求解即可．

试题解析：如图，分别过点A、B作CD的垂线交CD于点E、F，令两条河岸之间的距离为h．

∵AE⊥CD，BF⊥CD，AB∥CD，AB=20，

∴AE=BF=h，EF=AB=20．

在Rt△ACE中，∵∠AEC=90°，∠ACE=30°，

∴tan∠ACE=，即tan30°=，

∴CE=h．

在Rt△BDF中，∵∠BFD=90°，∠BDF=45°，

∴DF=BF=h．

∵CD=70，

∴CE+EF+FD=70，

∴h+20+h=70，

∴h=25（﹣1）≈18．

答：两条河岸之间的距离约为18米．