
【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,再从中任意摸出1个球是白球的概率为![]() .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法表示两次摸到球的所有可能结果,并求两次摸到的球都是白球的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
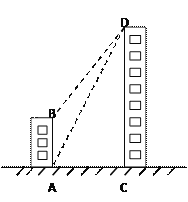
【题目】如图,一栋居民楼AB的高为16米,远处有一栋商务楼CD,小明在居民楼的楼底A处测得商务楼顶D处的仰角为![]() ,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为
,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为![]() .其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
.其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
(参考数据: ![]() ,
, ![]() .结果精确到0.1米)
.结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
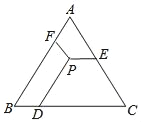
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;

(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5![]() 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
(2)如图2,矩形ABCD中,AB=![]() ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF![]() DE于点F,若DE=
DE于点F,若DE=![]() CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;
(3)如图3,在Rt![]() ABC中,
ABC中,![]() ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
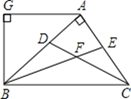
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com