
����Ŀ���Ķ����⣺
��A��B��CΪ�����������ҵ�C��A��B֮�䣬����C��A�ľ����ǵ�C��B�ľ����3�������ǾͳƵ�C�ǣ�A��B���ĺõ㣮

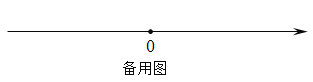
���磬��ͼ1����A��ʾ����Ϊ��2����B��ʾ����Ϊ2����ʾ1�ĵ�C��A�ľ�����3����B�ľ�����1����ô��C�ǣ�A��B���ĺõ㣻���磬��ʾ��1�ĵ�D��A�ľ�����1����B�ľ�����3����ô��D�Ͳ��ǣ�A��B���ĺõ㣬����D�ǣ�B��A���ĺõ㣮
֪ʶ���ã�
��1����M��NΪ���������㣬��M����ʾ����Ϊ��6����N����ʾ����Ϊ2��
�� ����ʾ�ĵ��ǣ�M��N���ĺõ㣻
�� ����ʾ�ĵ��ǣ�N��M���ĺõ㣻
��2������A��ʾ����Ϊa����B��ʾ����Ϊb����B�ڵ�A���ұߣ��ҵ�B��A�� C֮�䣬��B�ǣ�C��A���ĺõ㣬���C����ʾ�������ú�a��b�Ĵ���ʽ��ʾ����
��3����A��BΪ���������㣬��A����ʾ����Ϊ��33����B����ʾ����Ϊ27������һֻ��������P�ӵ�A��������ÿ��6����λ���ٶ������˶����˶�ʱ��Ϊt�룮���P��A��B��ǡ��һ����Ϊ��������ĺõ㣬��t��ֵ��
���𰸡���1��0����4����2��![]() ����3��
����3��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ݶ��巢�֣��õ㵽M�ǵ�N�ľ����3�����Ӷ��ó����ۣ����ݶ��巢�֣��õ㵽N�ǵ�M�ľ����3�����Ӷ��ó����ۣ�
��2�����C����ʾ����Ϊc���������г���ϵʽ������⣻
��3����������ۣ��г���ϵʽ����⼴��.
��1���������⣬��
��0����ʾ�ĵ��ǡ�M��N���ĺõ㣻
��-4����ʾ�ĵ��ǡ�N��M���ĺõ㣻
��2�����C����ʾ����Ϊc���������
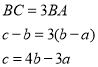
��3��������ã�AB=60
��P�ǡ�A��B���ĺõ�
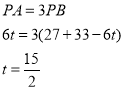
��P�ǡ�B��A���ĺõ�
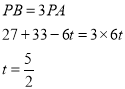
��B�ǡ�A��P���ĺõ�
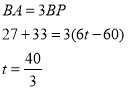
��B�ǡ�P��A���ĺõ�

��:��![]() ʱ, P��A��B��ǡ��һ����Ϊ��������ĺõ�.
ʱ, P��A��B��ǡ��һ����Ϊ��������ĺõ�.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݲ��ش����⣺
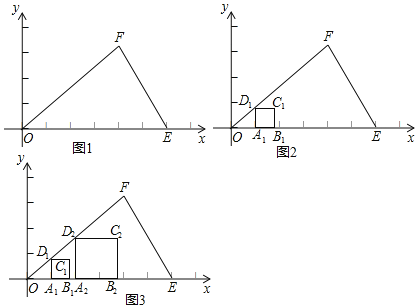
��ͼ1����ƽ��ֱ������ϵxOy�У���һ����OEF��Ҫ���ڡ�OEF����һ���ڽ�������ABCD��ʹ������A��B���������ڡ�OEF��OE���ϣ�����������C��D�ֱ���EF��OF�������ϣ�
С���е�Ҫʹ�ı��ε��ĸ�����ͬʱ��������������Щ���ѣ������������ı��ε��������������������������Ȼ���һ�������������������α��ϵ������Σ���ͼ2�������������ڡ�OEF�ڻ���һ�������������Σ���ͼ3��������������ٶһЩ�����������Σ����ܷ�����Щ��Cλ�õ�����ͼ�Σ��������ͼ�ξ��ܻ��������������������ˣ�
��1������Ҳʵ��һ�£��ٶ���������������Σ�����С��������Щ��C���е�ͼ������ ����
��2������ο�����˼·������������⣺���E��F���������ֱ�ΪE��6��0����F��4��3����
�ٵ�A1�������ǣ�1��0��ʱ����C1���������� ����
�ڵ�A2�������ǣ�2��0��ʱ����C2���������� ����
�۽�ϣ�1���в��룬���������ABCD�Ķ���D�����꣬��ͼ3�л�������������������ABCD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺(![]() )��2��
)��2��![]() +��
+��![]() ��4��0��
��4��0��![]() cos45�㣮
cos45�㣮
���𰸡�1
�������������������ԭʽ�ĵ�һ����ݸ�����ָ���ݵ����廯�ڶ����������ƽ�����Ķ������9������ƽ�����������������ָ����ʽ�������һ����������ǵ����Ǻ���ֵ���ϲ������ֵ.
���������ԭʽ=4��3+1��![]()
=2��1
=1��
�����͡������
��������
16
����Ŀ��������������������������һ�⣺�����ж���ͬ�������������ߣ������������Ҷ��У�������ʮ����б�������һᣮ�ʼ����и���������������˵����֪�ס��Ҷ���ͬʱ��ͬһ��
����������ٶ�Ϊ7���ҵ��ٶ�Ϊ3����һֱ���ߣ�����������10��������б��ƫ����������һ�κ�������������ô����ʱ�������Ҹ����˶�Զ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD����ACD�Ľ�ƽ���߽��ڵ�P������A = 50��,��D =10�������P�Ķ���Ϊ( )
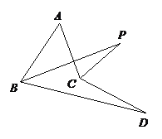
A.15��B.20��C.25��D.30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƷ���˶�Ь�����̹���A��B������ʽ�˶�Ь��������۳���ɻ���48000Ԫ����֪����A���˶�Ь��������B���˶�Ь������2�����������˶�Ь�Ľ��ۡ�������±���ʾ��
��ʽ �۸� | A | B |
���ۣ�Ԫ/˫�� | 100 | 120 |
��ۣ�Ԫ/˫�� | 250 | 300 |
��1���������˶�Ь����������˫��
��2�����A���˶�Ь�����9�۳��ۣ�B���˶�Ь�����8�۳��ۣ���ô�����˶�Ьȫ���۳���������������Ȱ���۳������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Сһ����ֱ���������ص���һ�𣬽�����һ�����������ŵ�B��C����ƽ�Ƶ�������DEF��λ�ã�AB��9��DH��3��ƽ�ƾ���Ϊ4������Ӱ���ֵ������_____��
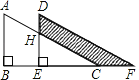
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Կ�չ��ѧ��ÿ�����1Сʱ���������ij��ѧ����ѧУʵ���������������A����ӣ�B������C���ܲ���D�����������˶���Ŀ��Ϊ���˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼͳ��ͼ������ͼ����Ϣ����������⣺
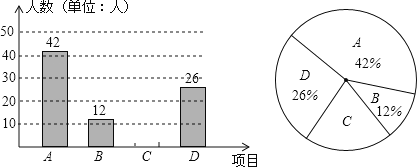
��1����У���ε����У��������˶�����ѧ����
��2���뽫����ͳ��ͼ����������
��3���ڱ��ε����ѧ���������ȡ1�ˣ���ϲ�����ܲ����ĸ����ж��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���һЩƹ�����ƹ�����ģ��˽���Ϣ���£��ס��������̵����ͬ��Ʒ�Ƶ�ƹ�����ƹ�����ģ�ƹ������ÿ������30Ԫ��ƹ����ÿ�ж���5Ԫ����Ǣ̸����ÿ��һ��������һ��ƹ�����ҵ�ȫ�������۵�9�۳��ۣ��ð�������5����ƹ�������ɺ�(������5��)�ʣ�
��1��������ƹ����x��ʱ�������Żݰ취��Ӧ�������Ԫ��(�ú�x�Ĵ���ʽ��ʾ)��
��2�����Ҫ����15��ƹ��������ȥ������£������ȥ�ļ��̵깺��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չѧ���ĺ�������������ѧ�����ۺ�������ijѧУ�ƻ���������ѡ�Σ��������赸���滭���鷨��ѧУ��ȡ��������ķ��������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ����Ե������������������Ƴ�����������������ͳ��ͼ������ͼ��������Ϣ����������⣺
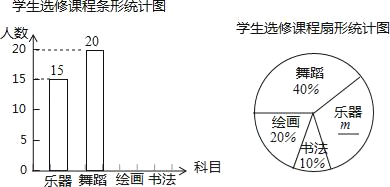
��1�����ε����ѧ�������� ���ˣ�������ͳ��ͼ�У�m��ֵ���� ����
��2��������ͳ��ͼ����������
��3���ڱ������ѧ���У�ѡ���鷨����2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ����ѧУ�μ�ij������֯���鷨�����д������ȡ��2��ͬѧǡ����1����ͬѧ��1��Ůͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com