
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
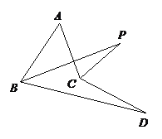
A.15°B.20°C.25°D.30°
科目:初中数学 来源: 题型:
【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一,在平面里有两点![]() ,
,![]() ,若
,若![]() 为起点,
为起点,![]() 为终点,则把有方向且有长度的线段
为终点,则把有方向且有长度的线段![]() 叫做向量,记为:
叫做向量,记为:![]() ,并且可用坐标表示这个向量,表示方法为:
,并且可用坐标表示这个向量,表示方法为:
![]() ,向量
,向量![]() 的长度可以表示成
的长度可以表示成![]()
例如:![]() ,
,![]() 则
则![]() ,
,
即![]() 所以
所以![]()
材料二:若![]() ,
,![]() ,则
,则![]()
若![]() 时,则
时,则![]() .
.
根据材料解决下列问题:
已知![]() 中,
中,![]() ,
,![]() ,
,![]()
(1)![]() ________
________ ![]() ___________
___________
(2)当![]() 时,求证:
时,求证:![]() 是直角三角形.
是直角三角形.
(3)若![]() ,
,![]() ,求使
,求使![]() 恒成立的
恒成立的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2![]() , AC=3
, AC=3![]() , BC=6,则⊙O的半径是( )
, BC=6,则⊙O的半径是( )
A.3
B.4
C.4![]()
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架![]() 的云梯
的云梯![]() 斜靠在一竖直的墙
斜靠在一竖直的墙![]() 上,这时
上,这时![]() 为
为![]() .
.
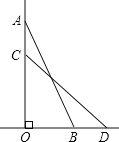
(1)求这个梯子的底端距墙的垂直距离有多远;
(2)当![]() ,且
,且![]() 时,AC的长是多少米;
时,AC的长是多少米;
(3)如果梯子![]() 的底端向墙一侧移动了2米,那么梯子的顶端向上滑动的距离是多少米?
的底端向墙一侧移动了2米,那么梯子的顶端向上滑动的距离是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下表:
型号 | 进价(元/只) | 售价(元/只) |
| 10 | 12 |
| 15 | 23 |
(1)该店用1300元可以购进![]() ,
,![]() 两种型号的文具各多少只?
两种型号的文具各多少只?
(2)若把(1)中所购进![]() ,
,![]() 两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点分别在四条平行线 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 上,这四条直线中相邻两条之间的距离依次为
上,这四条直线中相邻两条之间的距离依次为 ![]() 、
、 ![]() 、
、 ![]() (
( ![]() >0,
>0, ![]() >0,
>0, ![]() >0).
>0).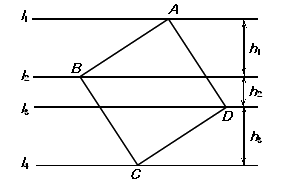
(1)求证: ![]() =
= ![]() ;
;
(2)设正方形ABCD的面积为S,求证:S= ![]() ;
;
(3)若 ![]() ,当
,当 ![]() 变化时,说明正方形ABCD的面积S随
变化时,说明正方形ABCD的面积S随 ![]() 的变化情况.
的变化情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com