
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2![]() , AC=3
, AC=3![]() , BC=6,则⊙O的半径是( )
, BC=6,则⊙O的半径是( )
A.3
B.4
C.4![]()
D.2![]()
【答案】D
【解析】解 :延长AC交⊙O于F,连接FD. 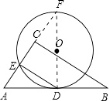
∵∠C=90°,DE∥BC,
∴∠DEF=90°,
∴FD是圆的直径.
∵AB切⊙O于D,
∴FD⊥AB.
∵DE∥BC,
∴△ADE∽△ABC.
∴AE∶AC=DE∶BC,即2∶3=DE∶6,
∴DE=4.
∵∠ADF=90°,DE⊥AF,
∴∠DEF=∠AED=90°;∠A+∠F=90°,∠A+∠ADE=90°;
∴∠F=∠ADE
∴△ADE∽△DFE,
∴DE∶FE=AE∶DE
∴DE2=AEEF,即42= 2![]() EF,
EF,
∴EF=4![]()
∴DF=![]()
OD=![]()
∴半径为![]()
延长AC交⊙O于F,连接FD. 根据二直线平行同旁内角互补得出∠DEF=90°,根据圆周角定理得出FD是圆的直径.根据切线的性质得出FD⊥AB.根据平行于三角形一边的直线截其它两边所截得的三角形与原三角形相似得出△ADE∽△ABC.根据相似三角形对应边成比例得出AE∶AC=DE∶BC,即2∶3=DE∶6,进而得出DE的长度,然后再判断出△ADE∽△DFE,根据相似三角形对应边成比例得出DE∶FE=AE∶DE,即DE2=AEEF,即42= 2EF,算出EF的长度,根据勾股定理得出DF的长度,从而得出该圆的半径。


科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
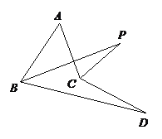
A.15°B.20°C.25°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() ∥
∥ ![]() ∥
∥ ![]() ,且
,且 ![]() 与
与 ![]() 的距离为1,
的距离为1, ![]() 与
与 ![]() 的距离为2,等腰 △ABC的顶点分别在直线
的距离为2,等腰 △ABC的顶点分别在直线 ![]() ,
, ![]() ,
, ![]() 上,AB=AC,∠BAC=120° ,则等腰三角形的底边长为。
上,AB=AC,∠BAC=120° ,则等腰三角形的底边长为。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2﹣8x﹣6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1 , 将C1向左平移得C2 , C2与x轴交于点B,D.若直线y=﹣x+m与C1 , C2共有3个不同的交点,则m的取值范围是( )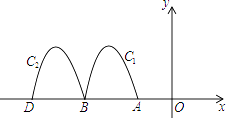
A.﹣3<m<﹣ ![]()
B.![]()
C.﹣2<m< ![]()
D.﹣3<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。
(1)求A、B两种型号的汽车每辆进价分别为多少方元?
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案;
(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com