
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
【答案】(1)5-t,10-2t;(2)8;(3)t=12.5或7.5.
【解析】试题分析:(1)先求出当0<t<5时,P点对应的有理数为10+t<15,Q点对应的有理数为2t<10,再根据两点间的距离公式即可求出BP,AQ的长;
(2)先求出当t=2时,P点对应的有理数为10+2=12,Q点对应的有理数为2×2=4,再根据两点间的距离公式即可求出PQ的长;
(3)由于t秒时,P点对应的有理数为10+t,Q点对应的有理数为2t,根据两点间的距离公式得出PQ=|2t﹣(10+t)|=|t﹣10|,根据PQ=![]() AB列出方程,解方程即可.
AB列出方程,解方程即可.
试题解析:解:(1)∵当0<t<5时,P点对应的有理数为10+t<15,Q点对应的有理数为2t<10,∴BP=15﹣(10+t)=5﹣t,AQ=10﹣2t.
故答案为:5﹣t,10﹣2t;
(2)当t=2时,P点对应的有理数为10+2=12,Q点对应的有理数为2×2=4,所以PQ=12﹣4=8;
(3)∵t秒时,P点对应的有理数为10+t,Q点对应的有理数为2t,∴PQ=|2t﹣(10+t)|=|t﹣10|,∵PQ=![]() AB,∴|t﹣10|=2.5,解得t=12.5或7.5.
AB,∴|t﹣10|=2.5,解得t=12.5或7.5.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】2016年鄞州区财政收入仍保持持续增长态势,全年财政收入为373.9亿元,其中373.9亿元用科学记数法表示为( )
A.373.9×108元
B.37.39×109元
C.3.739×1010元
D.0.3739×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.邻边之比相等的两个平行四边形一定相似B.邻边之比相等的两个矩形一定相似
C.对角线之比相等的两个平行四边形一定相似D.对角线之比相等的两个矩形一定相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的三边是三个连续的奇数,最长边是2k+5(k为大于1的整数),则其它两边分别分别是 和 ,猜想:这个三角形的最长边与最短边之和与第三边有何关系,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
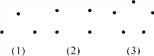
【题目】如图.
(1)试验观察:
如果每过两点可以画一条直线,那么:
第(1)组最多可以画_______条直线;
第(2)组最多可以画_______条直线;
第(3)组最多可以画_______条直线;
(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在1条直线上,那么最多可以画![]() 条直线;(用含n的代数式表示)
条直线;(用含n的代数式表示)
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握________次手.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学足球队9名队员的年龄情况如下:
年龄(单位:岁) | 14 | 15 | 16 | 17 |
人数 | 1 | 4 | 2 | 2 |
则该队队员年龄的众数和中位数分别是( )
A. 15,15 B. 15,16 C. 15,17 D. 16,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com