
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动。设运动时间为t(s),解答下列问题。
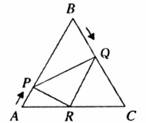
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ?
解:(1)△BPQ是等边三角形,
当t=2时,AP=2×1=2,BQ=2×2=4。
∴BP=AB-AP=6-2=4。
∴BQ=BP,
又∵∠B=60º,
∴△BPQ是等边三角形。
(2)过Q作QE⊥ AB,垂足为E。

由QB=2t,得QE=2t?sin60º=![]() t,
t,
由AP=t,得PB=6-t,
∴![]() 。
。
(3)∵QR∥BA,
∴∠QRC=∠A=60º,∠RQC=∠B=60º。
又∵∠C=60º,
∴△QRC是等边三角形
∴QR=RC=QC=6-2t。
∵BE=BQ?cos60º=![]() ,
,
∴EP=AB-AP-BE=6-t-t=6-2t。
∴EP∥QR,EP=QR。
∴四边形EPRQ是平行四边形,
∴PR=EQ=![]() t。
t。
又∵∠PEQ=90º,
∴∠APR=∠PRQ=90º,
∴△APR∽△PRQ,
∴∠QPR=∠A=60º,
∴![]() ,即
,即![]() ,
,
解得![]()
∴当![]() 时,△APR∽△PRQ。
时,△APR∽△PRQ。


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
 的坐标为(-1,0).
的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:
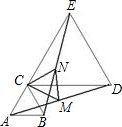 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com