
【题目】如图,AB为⊙O的直径,点D为AB下方⊙O上一点,点C为弧ABD的中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长度.



【答案】(1)证明见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接AD,如图1,设∠BDC=α,∠ADC=β,根据圆周角定理得到∠CAB=∠BDC=α,由AB为⊙O直径,得到∠ADB=90°,根据余角的性质即可得到结论;
(2)根据已知条件得到∠ACE=∠ADC,等量代换得到∠ACE=∠CAE,于是得到结论;
(3)如图2,连接OC,根据圆周角定理得到∠COB=2∠CAB,等量代换得到∠COB=∠ABD,根据相似三角形的性质得到OH=5,根据勾股定理得到AB=![]() =26,由相似三角形的性质即可得到结论.
=26,由相似三角形的性质即可得到结论.
(1)连接AD.如图1,设∠BDC=α,∠ADC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,∴![]() =
=![]() ,∴∠ADC=∠DAC=β,∴∠DAB=β﹣α,
,∴∠ADC=∠DAC=β,∴∠DAB=β﹣α,
∵AB为⊙O直径,∴∠ADB=90°,∴α+β=90°,∴β=90°﹣α,∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),∴∠ABD=2α,∴∠ABD=2∠BDC;

(2)∵CH⊥AB,∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,∴∠ACE=∠ADC,
∵∠CAE=∠ADC,∴∠ACE=∠CAE,∴AE=CE;
(3)如图2,连接OC,∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,∴△OCH∽△ABD,∴![]() ,
,
∵OH=5,∴BD=10,∴AB=![]() =26,∴AO=13,∴AH=18,
=26,∴AO=13,∴AH=18,
∵△AHE∽△ADB,∴![]() ,即
,即![]() =
=![]() ,∴AE=
,∴AE=![]() ,∴DE=
,∴DE=![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 026,则n的值为( ).
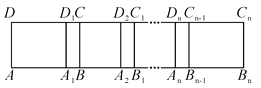
A. 407B. 406C. 405D. 404
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字:![]() ,1,2,
,1,2,![]() 的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法![]() 只选其中一种
只选其中一种![]() ,表示两次抽出卡片上的数字的所有结果;
,表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点![]() 落在双曲线
落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
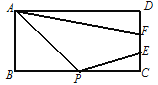
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从德州市2013年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:
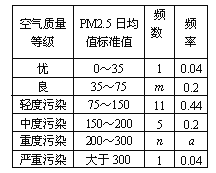
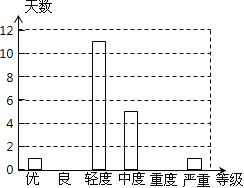
(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良;
(3)请你结合图表评价一下我市的空气质量情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=4![]() ,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD 上,则旋转中心的坐标为_______ .
,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD 上,则旋转中心的坐标为_______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=36°,将△ABC绕平面中的某一点D按顺时针方向旋转一定角度得到△![]()
![]()
![]() .
.
(1)若旋转后的图形如图所示,请在图中用尺规作出点D,请保留作图痕迹,不要求写作法;
(2)若将△ABC按顺时针方向旋转到△![]()
![]()
![]() 的旋转角度为
的旋转角度为![]() (0°<
(0°<![]() <180°),且AC⊥
<180°),且AC⊥![]()
![]() ,直接写出旋转角度
,直接写出旋转角度![]() 的值为_____.
的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.
(Ⅰ)若BP=QC,求证:AP=PQ;
(Ⅱ)若AP=PQ,求∠APQ的度数.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com