Question

【题目】如图，在△BDE中，∠BDE=90°，BD=4，点D的坐标是(5，0)，∠BDO=15°，将△BDE旋转到△ABC的位置，点C在BD 上，则旋转中心的坐标为_______ .

Answer 1

【答案】(3，2)

【解析】

根据旋转的性质，AB与BD的垂直平分线的交点即为旋转中心P，连接PD，过P作PF⊥x轴于F，再根据点C在BD上确定出∠PDB=45°并求出PD的长，然后求出∠PDO=60°，根据直角三角形两锐角互余求出∠DPF=30°，根据直角三角形30°角所对的直角边等于斜边的一半可得DF=PD，利用勾股定理列式求出PF，再求出OF，即可得到点P，即旋转中心的坐标．

如图，AB与BD的垂直平分线的交点即为旋转中心P，

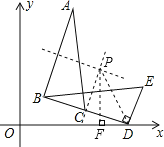
连接PD，过P作PF⊥x轴于F，

∵点C在BD上，

∴点P到AB、BD的距离相等，都是BD，即×4=2，

∴∠PDB=45°，

PD=×2=4，

∵∠BDO=15°，

∴∠PDO=45°+15°=60°，

∴∠DPF=30°，

∴DF=PD=×4=2，

∵点D的坐标是（5，0），

∴OF=OD-DF=5-2=3，

由勾股定理得，PF=，

∴旋转中心的坐标为（3，2）．

故答案为：（3，2）．