
【题目】如图,直线y=2x与反比例函数y=![]() (x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标.

【答案】(1)32;(2)5;(3)点D的坐标为(10,0)或(![]() ,0).
,0).
【解析】
(1)先把A(4,n)代入y=2x,求出n的值,再把A(4,8)代入y=![]() 求出k的值即可;
求出k的值即可;
(2)设AC=x,则OC=x,BC=8﹣x,由勾股定理得:OC2=OB2+BC2,即可求出x的值;
(3)设点D的坐标为(x,0),分两种情况:①当x>4时,②当0<x<4时,根据三角形的面积公式列式求解即可.
解(1)∵直线y=2x与反比例函数y=![]() (k≠0,x>0)的图象交于点A(4,n),
(k≠0,x>0)的图象交于点A(4,n),
∴n=2×4=8,
∴A(4,8),
∴k=4×8=32,
∴反比例函数为y=![]() .
.
(2)设AC=x,则OC=x,BC=8﹣x,
由勾股定理得:OC2=OB2+BC2,
∴x2=42+(8﹣x)2,
x=5,
∴AC=5;
(3)设点D的坐标为(x,0)
分两种情况:
①当x>4时,如图1,
∵S△OCD=S△ACD,
∴![]() ODBC=
ODBC=![]() ACBD,
ACBD,
3x=5(x﹣4),
x=10,
②当0<x<4时,如图2,
同理得:3x=5(4﹣x),
x=![]() ,
,
∴点D的坐标为(10,0)或(![]() ,0).
,0).


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=4![]() ,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD 上,则旋转中心的坐标为_______ .
,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD 上,则旋转中心的坐标为_______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
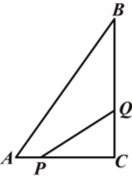
【题目】如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.
(Ⅰ)若BP=QC,求证:AP=PQ;
(Ⅱ)若AP=PQ,求∠APQ的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
(1)请判断线段AE和BD的数量关系和位置关系,并证明;
(2)若已知∠AED=135°,设∠AEC=α,当△BDE为等腰三角形时,求α的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为![]() ,水位高度变量为
,水位高度变量为![]() ,下列图象中最符合故事情景的大致图象是( )
,下列图象中最符合故事情景的大致图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com