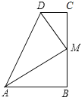
【题目】如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，∠CMD=35°，∠MAB的度数是________．
【答案】35°．
【解析】
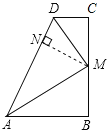
过点M作MN⊥AD于N，根据角平分线的性质可得MC=MN，可求出MB=MN，再根据到角的两边距离相等的点在角的平分线上判断出AM是∠BAD的平分线，然后求出∠AMB，再根据直角三角形两锐角互余求解即可．
解：如图，过点M作MN⊥AD于N，
∵∠C=90°，DM平分∠ADC，
∴MC=MN，
∴∠CMD=∠NMD =35°，
∵M是BC的中点，
∴MB=MC，
∴MB=MN，
∵∠B=90°，
∴AM是∠BAD的平分线，∠AMB=∠AMN，
∵∠CMD=∠NMD =35°，
∴∠AMB=
（180°-35°×2）=55°，
∴∠MAB=90°-∠AMB=90°-55°=35°．
故答案为：35°．
捷径训练检测卷系列答案
小夫子全能检测系列答案科目：初中数学 来源： 题型：
【题目】前几天，在青岛召开了举世目的“上合”会议，会议之前需要印刷批宣传彩页．经招标，
印务公司中标，该印务公司给出了三种方案供主办方选择：
方案一：每份彩页收印刷费
元．
方案二：收制版费
元，外加每份彩页收印刷费
元．
方案三：印数在份以内时，每份彩页收印刷费
元，超过份时，超过部分按每份
元收费．
（1）分别写出各方案的收费
（元）与印刷彩页的份数
（份）之间的关系式．
（2）若预计要印刷
份的宣传彩页，请你帮主办方选择一种合算的方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，阳光通过窗口照到教室内，竖直窗框在地面上留下2.1 m长的影子如图所示，已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m，窗口底边离地面的距离BC=1.2 m，试求窗口的高度（即AB的值）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CD是经过∠BCA顶点C的一条直线，且直线CD经过∠BCA的内部，点E，F在射线CD上，已知CA=CB且∠BEC=∠CFA=∠α．
（1）如图1，若∠BCA=80°，∠α=90°，问EF=BE-AF，成立吗？说明理由．
（2）将（1）中的已知条件改成∠BCA=∠β，∠α+∠β=180°（如图2），问EF=BE-AF仍成立吗？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：四边形ABCD中，∠ABC=∠ADC=90°，AB=BC，连接BD．
（1）画出示意图；
（2）请问：DB平分∠ADC吗？请给出结论，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=2x与反比例函数y=
（x＞0）的图象交于点A（4，n），AB⊥x轴，垂足为B．
（1）求k的值；
（2）点C在AB上，若OC=AC，求AC的长；
（3）点D为x轴正半轴上一点，在（2）的条件下，若S△OCD=S△ACD，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，规定把一个三角形先沿x轴翻折，再向右平移两个单位称为一次变换，如图，已知等边三角形ABC的顶点B、C的坐标分别是，（-1，-1），（-3，-1），把三角形ABC经过连续9次这样的变换得到三角形A’B’C’，则点A的对应点A’的坐标是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
