
【题目】如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.

(1)如图1,若∠BCA=80°,∠α=90°,问EF=BE-AF,成立吗?说明理由.
(2)将(1)中的已知条件改成∠BCA=∠β,∠α+∠β=180°(如图2),问EF=BE-AF仍成立吗?说明理由.
【答案】(1)EF=BE-AF成立,理由见解析;(2)EF=BE-AF成立,理由见解析.
【解析】
(1)根据已知条件可得∠B=∠ACE,证明△BCE≌△ CAF,则有BE=CF,AF=EC,所以可得EF=BE-AF;
(2)根据∠BCA=∠β,∠BEC=∠α=180°-∠β可求得∠B=∠ACE,则可证明△BCE≌△ CAF,则有BE=CF,AF=EC,所以可得EF=BE-AF.
(1)EF=BE-AF成立,理由如下:
∵∠BCA=80°(已知),
∴∠BCE+∠ACE=80°
∵∠BEC=∠α=100°(已知),
∴∠BEF=180°-100°=80°(平角定义).
∴∠B+∠BCE=80°(三角形外角和定理)
∴∠B=∠ACE(等量代换).
在△BCE和△CAF中,
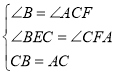
∴△BCE≌△ CAF(AAS)
∴BE=CF,AF=EC(全等三角形对应边相等).
∴EF=CF-CE=BE-AF(等量代换).
(2)EF=BE-AF成立,理由如下:
∵∠BCA=∠β,
∴∠BCE+∠ACE=∠β
∵∠BEC=∠α=180°-∠β,
∴∠BEF=180°-∠α=∠β.
∴∠B+∠BCE=∠β.
∴∠B=∠ACE
在△BCE和△CAF中,
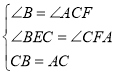
∴△BCE≌△ CAF(AAS)
∴BE=CF,AF=EC
∴EF=CF-CE=BE-AF.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
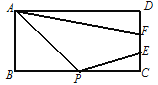
【题目】如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有( )
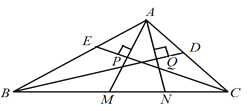
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
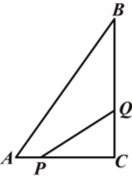
【题目】已知:等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.
(Ⅰ)若BP=QC,求证:AP=PQ;
(Ⅱ)若AP=PQ,求∠APQ的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() = .
= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com