
����Ŀ��˾���ڼ�ʻ����ʱ�����ֽ������������ɲ����Ҫһ��ʱ�䣬���ʱ��з�Ӧʱ�䣮֮�������ʻһ�ξ��룮���ǰ�˾���ӷ��ֽ������������ֹͣ����ʻ����ξ������ɲ��������(��ͼ)��
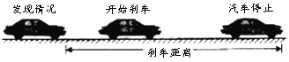
��֪������ɲ������![]() (��λ����)�복��
(��λ����)�복��![]() (��λ���ף���)֮�������¹�ϵ��
(��λ���ף���)֮�������¹�ϵ��![]() ������
������![]() Ϊ˾���ķ�Ӧʱ��(��λ����) ��
Ϊ˾���ķ�Ӧʱ��(��λ����) ��![]() Ϊ�ƶ�ϵ����ij����Ϊ����˾�����ƺ�ɲ������ı仯����ij���ͺŵ��������������������ݳ����ԣ���֪���ͺ��������ƶ�ϵ��
Ϊ�ƶ�ϵ����ij����Ϊ����˾�����ƺ�ɲ������ı仯����ij���ͺŵ��������������������ݳ����ԣ���֪���ͺ��������ƶ�ϵ��![]() �������־Ը����δ����ʱ�ķ�Ӧʱ��
�������־Ը����δ����ʱ�ķ�Ӧʱ��![]() �룮
�룮
��1����־Ը��δ���ƣ��ҳ���Ϊ16�ף��룬���������ɲ������Ϊ �� ��
��2����־Ը���ں���һƿơ�ư�Сʱ����16�ף�����ٶȼݳ���ʻ�����ɲ������Ϊ59.2�ף���ʱ��־Ը�ߵķ�Ӧʱ���� �룮
��3�������־Ը����10�ף���ij�����ʻ�����ƺ�Ӧʱ���ǵڣ�2��������������������ƺ��ɲ��������δ����ʱ��ɲ��������������˶��٣�
��4���������ʻ���ͺŵ�������16 �ף�����ٶ���ʻ, ������ǰ��46�״�ͣ��һ�����������㷴Ӧʱ����1. 3��.�����������Ƿ�ᷢ����β��? ��ͨ���������˵��.
���𰸡�(1)33.6��(2)2.1��(3)δ����ʱ: S=15,���ƺ�: S=31,������16�ף�(4)β
��������
��1����k=0.1��t=0.5��v=16������㼴�ɵõ�ɲ�����룻
��2����k=0.1��v=16��s=59.2����������ϵʽ�ɵ�t��ֵ��
��3����k=0.1��v=10��t=2.1��0.5�ֱ����������ϵʽ�ɵ�ɲ�����룬��������ɣ�
��4����k=0.1��v=16��t=1. 3����������ϵʽ�����![]() ��ֵ���ɣ�
��ֵ���ɣ�
�⣺��1����k=0.1��t=0.5��v=16ʱ��
s=0.5��16+0.1��162=33.6���ף���
�ʴ�Ϊ��33.6��
��2����k=0.1��v=16��s=59.2ʱ��
59.2=16t+0.1��162��
���t=2.1���룩��
�ʴ�Ϊ2.1��
��3����k=0.1��v=10��t=2.1ʱ��s=2.1��10+0.1��102=31���ף���
��k=0.1��v=10��t=0.5ʱ��s=0.5��10+0.1��102=15���ף���
31-15=16���ף���
��ɲ�����뽫��δ����ʱ����16�ף�
��4����k=0.1��v=16��t=1. 3ʱ��![]() =1.3��16+0.1��162=46.4���ף���
=1.3��16+0.1��162=46.4���ף���
46��46.4��
���ԣ����������ᷢ����β����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���ڵ�A(3,m).
���ڵ�A(3,m).
��1����k��m��ֵ��
��2����֪��P(n��n)(n>0)������P��ƽ����![]() ���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������
���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������![]() ��ͼ���ڵ�N.
��ͼ���ڵ�N.
�ٵ�n=1ʱ���ж��߶�PM��PN��������ϵ����˵�����ɣ�
����PN��PM����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�Ķ���Ϊÿ��20Ԫ���̳�Ϊ�˴����������������5�����ϣ���5���IJ��ִ�7�ۣ�
��1������������Ʒ�Ļ���y ��Ԫ���빺������x ������֮��ĺ�����ϵ��
��2����x=3��x=6ʱ������ֱ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
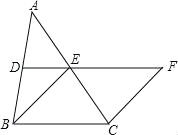
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���е㣬BE��2DE���ӳ�DE����F��ʹ��EF��BE������CF��
��1����֤���ı���BCFE�����Σ�
��2����CE��2����BCF��120����������BCFE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
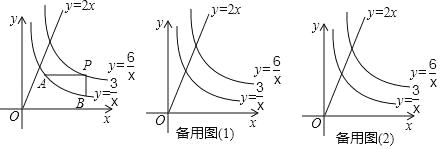
����Ŀ����֪��P��m��n���Ƿ���������y��![]() ��x��0����ͼ���ϵ�һ���㣬PA��x�ᣬPB��y�ᣬ�ֱ���������y��
��x��0����ͼ���ϵ�һ���㣬PA��x�ᣬPB��y�ᣬ�ֱ���������y��![]() ��x��0����ͼ���ڵ�A��B����C��ֱ��y��2x�ϵ�һ�㣮
��x��0����ͼ���ڵ�A��B����C��ֱ��y��2x�ϵ�һ�㣮
��1����A������Ϊ���� ������ ��������B������Ϊ���� ������ ���������ú�m�Ĵ���ʽ��ʾ��
��2���ڵ�P�˶��Ĺ����У�����AB��֤������PAB�������һ����ֵ������������ֵ��
��3���ڵ�P�˶��Ĺ����У��Ե�P��A��B��CΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ������ʱm��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DΪ��O��һ�㣬��C��ֱ��BA���ӳ����ϣ��ҡ�CDA=��CBD��
��1����֤��CD�ǡ�O�����ߣ�
��2������B����O�����߽�CD���ӳ����ڵ�E��BC=6�� ![]() ����BE�ij���
����BE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����֪����![]() ���������ϱ�ʾ5�ĵ���ԭ��(����ʾ0�ĵ�)֮��ľ���.����ʽ��
���������ϱ�ʾ5�ĵ���ԭ��(����ʾ0�ĵ�)֮��ľ���.����ʽ��![]() ,���������ϵ������DZ�ʾ6�ĵ����ʾ3�ĵ�֮��ľ���.����A��B�������Ϸֱ��ʾ��a��b,��A��B����ľ���ɱ�ʾΪ:|AB|=
,���������ϵ������DZ�ʾ6�ĵ����ʾ3�ĵ�֮��ľ���.����A��B�������Ϸֱ��ʾ��a��b,��A��B����ľ���ɱ�ʾΪ:|AB|=![]() .����
.����
������Ϣ���ش��������⣺
(1)�����ϱ�ʾ2��5������֮��ľ����� �������ϱ�ʾ-2��-5������֮��ľ����� .
��2����A��B�������Ϸֱ��ʾʵ��x��![]() .
.
���ô���ʽ��ʾA��B����֮��ľࣻ
�����![]() ,��x��ֵ.
,��x��ֵ.
��3��ֱ��д������ʽ![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����κ�����ͼ��A��0����6����B��4����6����C��6��0�����㣮
��1����������κ����Ľ���ʽ��
��2���ֱ�����AC��BC����tan��ACB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ACΪһ��ֱ�ߣ�O��AC��һ�㣬 OE��OF�ֱ�ƽ�֡�AOB�͡�BOC.
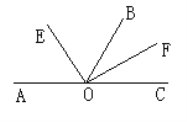
(1)��ͼ������AOB=120�������EOF�Ĵ�С;
(2)����AOB=60�������EOF= _______ ��;
(3)����ı��AOB�Ĵ�С����EOF�Ĵ�С��ı���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com