
【题目】已知一个二次函数的图象经过A(0,﹣6)、B(4,﹣6)、C(6,0)三点.
(1)求这个二次函数的解析式;
(2)分别联结AC、BC,求tan∠ACB.
【答案】(1)抛物线的解析式为y=![]() x2+2x﹣6;(2)tan∠ACB=
x2+2x﹣6;(2)tan∠ACB=![]() .
.
【解析】试题分析:
(1)设二次函数的解析式为:![]() ,把点A、B、C的坐标代入所设解析式列出方程组,解方程组求得a、b、c的值即可得到所求解析式;
,把点A、B、C的坐标代入所设解析式列出方程组,解方程组求得a、b、c的值即可得到所求解析式;
(2)如下图,作作BH⊥AC于H,易证△AOC是等腰直角三角形,从而可得AC=![]() ,∠OAC=45°,由此可得∠BAH=45°,从而可得△ABH是等腰直角三角形,由AB=4可得AH=BH=
,∠OAC=45°,由此可得∠BAH=45°,从而可得△ABH是等腰直角三角形,由AB=4可得AH=BH=![]() ,由此可得CH=AC-AH=
,由此可得CH=AC-AH=![]() ,这样在Rt△BCH中可得tan∠ACB=
,这样在Rt△BCH中可得tan∠ACB=![]() .
.
试题解析:
(1)设抛物线的解析式为y=ax2+bx+c,
根据题意得: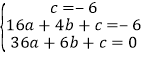 ,
,
解得: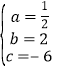 ,
,
∴抛物线的解析式为y=![]() x2+2x﹣6;
x2+2x﹣6;
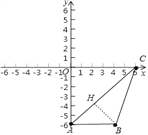
(2)作BH⊥AC于H,如图,
∵OA=OC,
∴△OAC为等腰直角三角形,
∴∠OAC=45°,AC=![]() OA=
OA=![]() ,
,
∵A(0,﹣6)、B(4,﹣6),
∴AB∥x轴,AB=4,
∴∠BAC=45°,
∴△ABH为等腰直角三角形,
∴AH=BH=![]() AB=
AB=![]() ,
,
∴CH=![]() ,
,
在Rt△BCH中,tan∠HCB=![]() ,
,
即tan∠ACB=![]() .
.


科目:初中数学 来源: 题型:
【题目】计算:
(1)3y2-2y+4y2;
(2)![]() +4-3st-4;
+4-3st-4;
(3)2(2ab+3a)-3(2a-ab);
(4)a2-[-4ab+(ab-a2)]-2ab.
(5).(-1)3-![]() ÷3×[3-(-3)2];
÷3×[3-(-3)2];
(6)![]() ×
×![]() ÷(-9+19);
÷(-9+19);
(7)-24×![]() ;
;
(8)(-81)÷![]() +
+![]() ÷(-16);
÷(-16);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间.之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).
已知汽车的刹车距离![]() (单位:米)与车速
(单位:米)与车速![]() (单位:米/秒)之间有如下关系:
(单位:米/秒)之间有如下关系:![]() ,其中
,其中![]() 为司机的反应时间(单位:秒) ,
为司机的反应时间(单位:秒) ,![]() 为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数
为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数![]() ,并测得志愿者在未饮酒时的反应时间
,并测得志愿者在未饮酒时的反应时间![]() 秒.
秒.
(1)若志愿者未饮酒,且车速为16米/秒,则该汽车的刹车距离为 米 .
(2)当志愿者在喝下一瓶啤酒半小时后,以16米/秒的速度驾车行驶,测得刹车距离为59.2米,此时该志愿者的反应时间是 秒.
(3)假如该志愿者以10米/秒的车速行驶,饮酒后反应时间是第(2)题求出来的量,则饮酒后的刹车距离与未饮酒时的刹车距离相比增加了多少?
(4)假如你驾驶该型号的汽车以16 米/秒的速度行驶, 发现正前方46米处停了一辆车,假设你反应时间是1. 3秒.问这两辆车是否会发生“追尾”? 请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
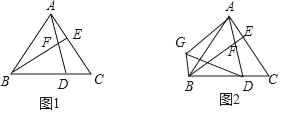
【题目】如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.
(1)求证:∠ABE=∠CAD;
(2)如图2,以AD为边向左作等边△ADG,连接BG.
ⅰ)试判断四边形AGBE的形状,并说明理由;
ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(或化简)下列各题
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(2)﹣42÷(﹣2)3+|﹣![]() |×(﹣8)
|×(﹣8)
(3)(﹣36)×(![]() )
)
(4)(﹣3)2﹣[(﹣![]() )+(﹣
)+(﹣![]() )]÷
)]÷![]()
(5)2(m﹣1)﹣(2m﹣3)
(6)(5ab+3a2)﹣2(a2+2ab)
(7)先化简,再求值:![]() x﹣2(x﹣
x﹣2(x﹣![]() y)+(﹣
y)+(﹣![]() x+
x+![]() y),其中x=﹣2,y=
y),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一”儿童节促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现.老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组:A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).
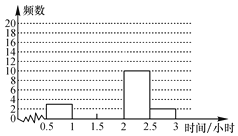
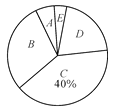
请根据图中提供的信息,解答下列问题:
(1)这次活动中学生做家务时间的中位数所在的组是____________;
(2)补全频数分布直方图;
(3)该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com